Wave Equation on Square Domain
This example shows how to solve the wave equation using the solvepde function.
The standard second-order wave equation is
To express this in toolbox form, note that the solvepde function solves problems of the form
So the standard wave equation has coefficients , , , and .
c = 1; a = 0; f = 0; m = 1;
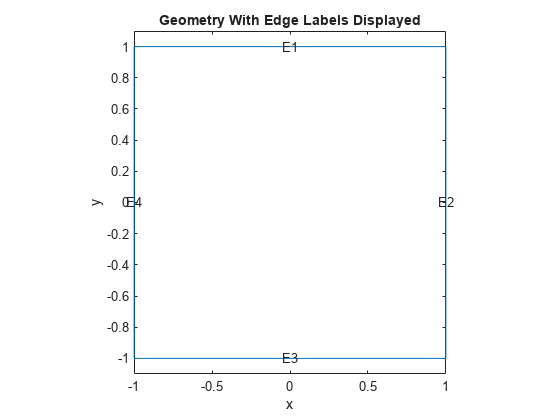
Solve the problem on a square domain. The squareg function describes this geometry. Create a model object and include the geometry. Plot the geometry and view the edge labels.
model = createpde; geometryFromEdges(model,@squareg); pdegplot(model,EdgeLabels="on"); xlim([-1.1 1.1]); ylim([-1.1 1.1]); title("Geometry With Edge Labels Displayed") xlabel("x") ylabel("y")
Specify PDE coefficients.
specifyCoefficients(model,m=m,d=0,c=c,a=a,f=f);
Set zero Dirichlet boundary conditions on the left (edge 4) and right (edge 2) and zero Neumann boundary conditions on the top (edge 1) and bottom (edge 3).
applyBoundaryCondition(model,"dirichlet",Edge=[2,4],u=0); applyBoundaryCondition(model,"neumann",Edge=[1 3],g=0);
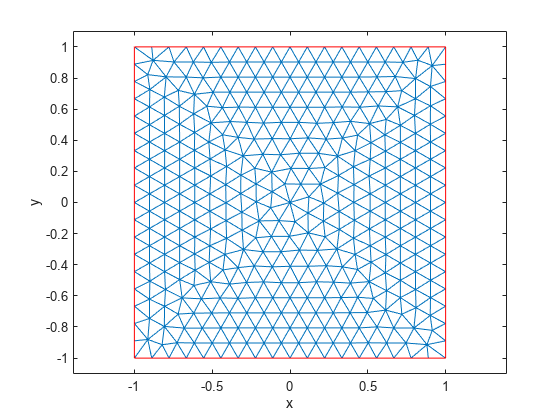
Create and view a finite element mesh for the problem.
generateMesh(model); figure pdemesh(model); ylim([-1.1 1.1]); axis equal xlabel x ylabel y
Set the following initial conditions:
.
.
u0 = @(location) atan(cos(pi/2*location.x)); ut0 = @(location) 3*sin(pi*location.x).*exp(sin(pi/2*location.y)); setInitialConditions(model,u0,ut0);
This choice avoids putting energy into the higher vibration modes and permits a reasonable time step size.
Specify the solution times as 31 equally-spaced points in time from 0 to 5.
n = 31; tlist = linspace(0,5,n);
Solve the problem.
result = solvepde(model,tlist); u = result.NodalSolution;
Create an animation to visualize the solution for all time steps. Keep a fixed vertical scale by first calculating the maximum and minimum values of u over all times, and scale all plots to use those -axis limits.
figure umax = max(max(u)); umin = min(min(u)); for i = 1:n pdeplot(model,XYData=u(:,i),ZData=u(:,i), ... ZStyle="continuous",Mesh="off"); axis([-1 1 -1 1 umin umax]); xlabel x ylabel y zlabel u M(i) = getframe; end
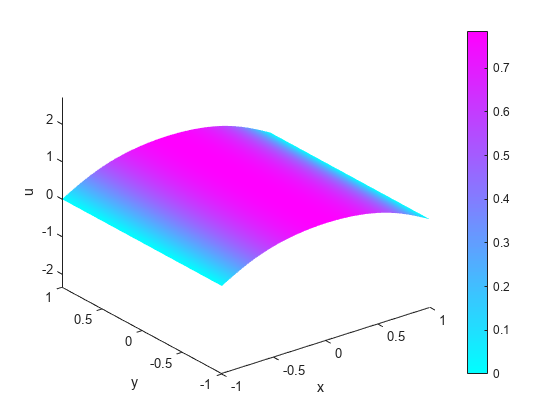
To play the animation, use the movie(M) command.