Digital Phase Locked Loop
This example shows how to model a digital phase locked loop using the Mixed-Signal Blockset™. In a digital phase locked loop, phase detection is performed by a time to digital converter (TDC), loop filtering is performed by a digital filter, and the oscillator is a digitally controlled oscillator (DCO). This example demonstrates a behavioral model of a TDC, using the BiquadFilter from the DSP System Toolbox™ as the digital loop filter, and using VCOs and DACs from the Mixed-Signal Blockset to model the DCO.
This example also demonstrates one method for designing the control loop of a digital PLL by using the PLL architectures from the Mixed-Signal Blockset to design an analog PLL and then translate the analog design to its digital equivalent.
Digital PLL
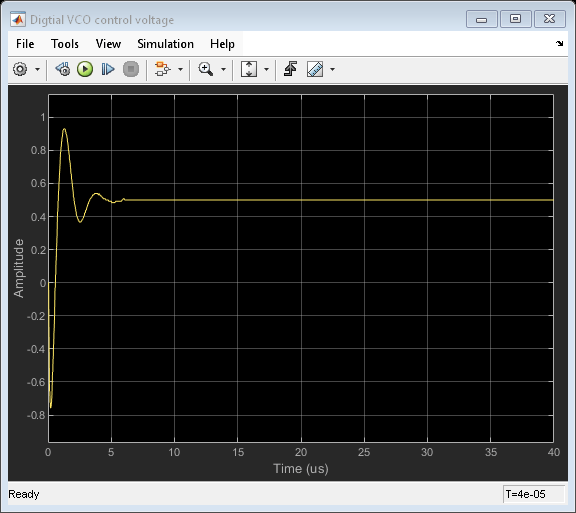
Open and run the example model of a digital PLL. Then select the PLL Testbench in the model and click the Plot phase noise button (or call the button's callback function). Save loop filter waveform and phase noise data for later comparison to analog PLL results.
open('DigitalPLL.slx'); simout = sim(bdroot); msblks.PLL.pllTBPlotPhaseNoiseButton([bdroot '/PLL Testbench']); dpll_vcntl = simout.dpll_vcntl; getDigitalPllPhaseNoise;


Time to Digital Converter
The behavioral model of the TDC uses triggered subsystems to sample the clock time at the rising edges of the reference clock and the PLL's fractional divider. It then calculates the difference between these two sampled clock times and converts to an eight bit integer output value. To model a digital feedback loop clocked by the reference, the output sample rate is set to the reference frequency using a zero order hold block.
open_system('DigitalPLL/TDC','force');

Digital Controlled Oscillator
The DCO model represents a circuit in which the control for a VCO is set by a digital to analog converter (DAC). The conversion in the DAC is triggered by the reference clock.
The phase noise impairment in the VCO is enabled. The DAC model can also model impairments. However the DAC impairments are not enabled in the example model.
You could alternatively model a DCO by directly setting a Mixed-Signal Blockset VCO's control voltage array to an array of consecutive integers that spans the range of digital input values. Then you can set the output frequency array to supply the output frequency for each possible input value.
open_system('DigitalPLL/DCO','force');

Digital Loop Filter
The loop filter is a BiquadFilter from the DSP System Toolbox. It is clocked at the reference clock frequency by the output port of the TDC.
The digital loop filter is designed using the automated design feature of the Integer N PLL with Single Modulus Prescaler model from the Mixed-Signal Blockset PLL Architectures library. An analog loop filter is designed to achieve a specified loop bandwidth and phase margin, then the circuit values and sample interval are translated to digital filter coefficients. To obtain the correct overall loop gain, a scale factor is applied to the biquad filter model of the loop filter.
The derivation of the loop gain scale factor parallels that of A Design Procedure for All-Digital Phase-Locked Loops Based on a Charge-Pump Phase-Locked-Loop Analogy.
The variables used in the derivation are
 Charge pump maximum current amplitude
Charge pump maximum current amplitude Analog loop filter transfer impedance
Analog loop filter transfer impedance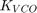 VCO sensitivity for both analog and digital PLLs
VCO sensitivity for both analog and digital PLLs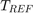 Reference clock period
Reference clock period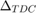 TDC time resolution
TDC time resolution Digital loop filter transfer function
Digital loop filter transfer function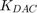 DAC gain
DAC gain
Note that for this example, the total range of the TDC is two reference clock periods.
The equation to make the loop gain of the analog and digital PLLs equal is:

Since the TDC and the DAC in this example have been configured to have the same number of bits, this equation reduces to:
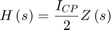
Since the function getSOSfromAnalogPLL included in this example produces filter coefficients that result in a filter gain  , the scale factor for the loop filter is
, the scale factor for the loop filter is  .
.
While the loop filter coefficients, input signal and output signal in this example are all double precision floating point, it would also be possible to use Fixed-Point Designer™ to model the entire digital feedback path using exactly the same digital precision as in the circuit design, thus obtaining even more precise evaluation of impairments such as quantization noise.
You can design and configure the digital loop filter by running the script:
%%%designDigitalLoopFilter;
Compare to Analog PLL
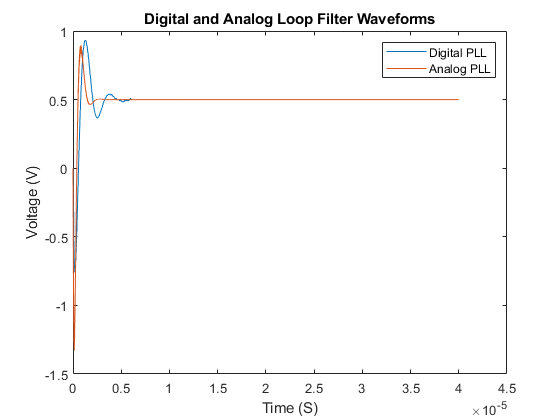
You can compare the loop acquisition of the analog PLL to that of the digital PLL. The additional high frequency ripple in the analog loop filter response is due to the charge pump waveform.
open('AnalogPLL.slx'); simout = sim(bdroot); apll_vcntl = simout.apll_vcntl; plotLoopFilterWaveforms; msblks.PLL.pllTBPlotPhaseNoiseButton([bdroot '/PLL Testbench']); plot(xdpll,ydpll,'LineWidth',2,'DisplayName','Digital PLL');