Explicit MPC Control of DC Servomotor with Constraint on Unmeasured Output
This example shows how to use explicit MPC to control a DC servomechanism under voltage and shaft torque constraints.
For a similar example that uses traditional implicit MPC, see DC Servomotor with Constraint on Unmeasured Output. For a related example with this plant, see Design MPC Controller for Position Servomechanism.
Define DC-Servo Motor Model
The mpcmotormodel function returns the plant model needed for the example. The linear open-loop dynamic model is defined in plant. The variable tau is the maximum admissible torque, this is going to be used as an output constraint.
[plant,tau] = mpcmotormodel;
Display basic plant characteristics.
size(plant) damp(plant)
State-space model with 2 outputs, 1 inputs, and 4 states.
Pole Damping Frequency Time Constant
(rad/seconds) (seconds)
8.23e-16 -1.00e+00 8.23e-16 -1.22e+15
-7.05e-01 + 7.31e+00i 9.59e-02 7.35e+00 1.42e+00
-7.05e-01 - 7.31e+00i 9.59e-02 7.35e+00 1.42e+00
-9.79e+00 1.00e+00 9.79e+00 1.02e-01
The plant control input is the DC voltage, the four state variables are the angular position and velocities of the load and the motor shaft. The measurable output is the angular position of the load. The second output, torque, is not measurable. For more information, see Design MPC Controller for Position Servomechanism.
Specify input and output signal types for the MPC controller.
plant = setmpcsignals(plant,'MV',1,'MO',1,'UO',2);
Specify Constraints
The manipulated variable is constrained between +/- 220 volts. Since the plant inputs and outputs are of different orders of magnitude, you also use scale factors to facilitate MPC tuning. Typical choices of scale factor are the upper/lower limit or the operating range.
MV = struct('Min',-220,'Max',220,'ScaleFactor',440);
Torque constraints of +|tau| and -|tau| are only imposed during the first three prediction steps. Also specify a scale factor for both outputs (load angle and torque).
OV = struct('Min',{Inf, [-tau;-tau;-tau;-Inf]},... 'Max',{Inf, [tau;tau;tau;Inf]},... 'ScaleFactor',{2*pi, 2*tau});
Specify Tuning Weights
The control task is to get zero tracking offset for the angular position. Since you only have one manipulated variable, the shaft torque is allowed to float within its constraint by setting its weight to zero.
Weights = struct('MV',0,'MVRate',0.1,'OV',[0.1 0]);
Create MPC controller
Create an MPC controller with sample time Ts, prediction horizon of 10 steps, and control horizon 2 steps.
Ts = 0.1; mpcobj = mpc(plant,Ts,10,2,Weights,MV,OV);
Calculate Closed Loop DC Gain Matrix
Calculate the steady state output sensitivity of the closed loop. A zero value means that the measured plant output can track the desired output reference setpoint.
cloffset(mpcobj)
-->Converting model to discrete time.
Assuming no disturbance added to measured output #1.
-->"Model.Noise" is empty. Assuming white noise on each measured output.
ans =
0
Explicit MPC
The constraints in the manipulated variables and outputs divide the state space of the MPC controller into many polyhedral regions such that within each region the MPC control law is a specific affine-in-the-state-and-reference function, with coefficients depending on the region. Explicit MPC calculates all these regions, and their relative control laws, offline. Online, the controller just selects and applies the precomputed solution relative to the current region, so it does not have to solve a constrained quadratic optimization problem at each control step. For more information on explicit MPC, see Explicit MPC.
Generate Explicit MPC Controller
Explicit MPC executes the equivalent explicit piecewise affine version of the MPC control law defined by the traditional MPC controller. To generate an explicit MPC controller from a traditional MPC controller, you must specify the range for each controller state, reference signal, manipulated variable and measured disturbance. Doing so ensures that the quadratic programming problem is solved in the space defined by these ranges. If at run time one of these independent variables falls outside of its range, the controller returns an error status and sets the manipulated variables to their last values. Therefore, it is important that you do not underestimate these ranges.
To generate suitable ranges, obtain some information on the controller states first.
Display size of the input and output disturbance models
To get the controller input and output disturbance models, use getindist and getoutdist, respectively.
size(getindist(mpcobj)) size(getoutdist(mpcobj))
State-space model with 0 outputs, 0 inputs, and 0 states. State-space model with 2 outputs, 0 inputs, and 0 states.
The controller does not use any disturbance model.
Display controller initial state
To display the controller initial states, use mpcstate.
mpcstate(mpcobj)
MPCSTATE object with fields
Plant: [0 0 0 0]
Disturbance: [1×0 double]
Noise: [1×0 double]
LastMove: 0
Covariance: [4×4 double]
As expected, the plant model used by the Kalman estimator has 4 states, and then there is one additional state needed to hold the last value of the manipulated variable.
Obtain a range structure for initialization
To create a range structure where you can specify the range for each state, reference, and manipulated variable, use generateExplicitRange.
range = generateExplicitRange(mpcobj);
Specify ranges for controller states, references, and manipulated variables
The MPC controller states include states from the plant model, disturbance model, noise model, and the last value of the manipulated variables, in that order. Setting the range of a state variable is sometimes difficult when the state does not correspond to a physical parameter. In that case, multiple runs of open-loop plant simulation with typical reference and disturbance signals, including model mismatches, are recommended to collect data that reflect the ranges of the states.
For this example, since the gear ration between the motor and load shafts is 20, overestimate the practical range of variation for the state variables (load angular position, load angular velocity, motor shaft angular position, motor shaft angular velocity), as follows.
range.State.Min(:) = [-4*pi -4*pi/Ts -4*pi*20 -4*pi*20/Ts]; range.State.Max(:) = [ 4*pi 4*pi/Ts 4*pi*20 4*pi*20/Ts];
Usually you know the practical range of the reference signals being used at the nominal operating point in the plant. The ranges used to generate the explicit MPC controller must be at least as large as the practical range. Note that the range for torque reference is fixed at 0 because the torque is not measurable, and therefore the controller does not use any reference signal for it.
range.Reference.Min = [-5;0]; range.Reference.Max = [5;0];
If manipulated variables are constrained, the ranges used to generate the explicit MPC controller must be at least as large as these limits.
range.ManipulatedVariable.Min = MV.Min - 1; range.ManipulatedVariable.Max = MV.Max + 1;
Create an explicit MPC controller with the specified ranges.
mpcobjExplicit = generateExplicitMPC(mpcobj,range)
Regions found / unexplored: 76/ 0 Explicit MPC Controller --------------------------------------------- Controller sample time: 0.1 (seconds) Polyhedral regions: 76 Number of parameters: 6 Is solution simplified: No State Estimation: Default Kalman gain --------------------------------------------- Type 'mpcobjExplicit.MPC' for the original implicit MPC design. Type 'mpcobjExplicit.Range' for the valid range of parameters. Type 'mpcobjExplicit.OptimizationOptions' for the options used in multi-parametric QP computation. Type 'mpcobjExplicit.PiecewiseAffineSolution' for regions and gain in each solution.
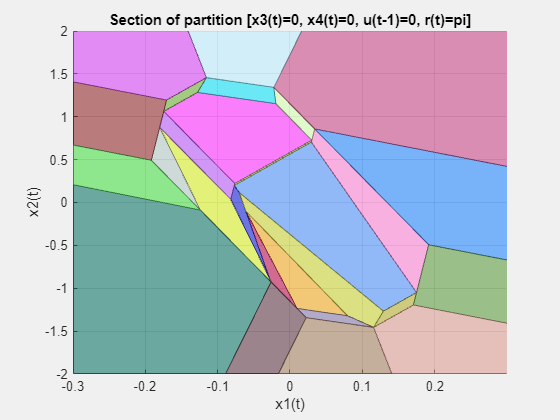
Plot Piecewise Affine Partition Along a Given Section
You can plot a 2-D section of the controller state space, and look at the regions in this section. For this example, plot the 2-D section of the state space defined by the first and second state variables (load angle and angular velocity). To do so you must first create a plot structure in which you fix all the other states (and reference signals) to specific values within their respective ranges.
To create a parameter structure where you can specify which 2-D section to plot afterwards, use the generatePlotParameters function.
plotpars = generatePlotParameters(mpcobjExplicit);
In this example, you plot the first state variable against the second state variable. All the other parameters must be fixed at values within their respective ranges.
Specify indexes of the third and fourth state variables and fix their values to zero.
plotpars.State.Index = [3 4]; plotpars.State.Value = [0 0];
Specify indexes the output reference signals and fix them to pi and 0, respectively.
plotpars.Reference.Index = [1 2]; plotpars.Reference.Value = [pi 0];
Specify index of the manipulated variable and fix its value to zero.
plotpars.ManipulatedVariable.Index = 1; plotpars.ManipulatedVariable.Value = 0;
Plot the specified 2-D section.
plotSection(mpcobjExplicit,plotpars); axis([-.3 .3 -2 2]); grid title('Section of partition [x3(t)=0, x4(t)=0, u(t-1)=0, r(t)=pi]') xlabel('x1(t)') ylabel('x2(t)')
Simulate Controller Using sim Function
Compare the closed-loop simulation results between the traditional (implicit) MPC and the explicit MPC controllers.
Tstop = 8; % seconds Tf = round(Tstop/Ts); % simulation iterations r = [pi 0]; % reference signal [y1,t1,u1] = sim(mpcobj,Tf,r); % simulation with traditional MPC [y2,t2,u2] = sim(mpcobjExplicit,Tf,r); % simulation with Explicit MPC
-->Converting model to discrete time. Assuming no disturbance added to measured output #1. -->"Model.Noise" is empty. Assuming white noise on each measured output.
The simulation results are identical.
fprintf('Difference between implicit and explicit MPC trajectories = %g\n',... norm(u2-u1)+norm(y2-y1));
Difference between implicit and explicit MPC trajectories = 8.16668e-12
Simulate Using Simulink
Simulate closed-loop control of the linear plant model in Simulink®. The Explicit MPC Controller block is configured to use mpcobjExplicit as its controller.
mdl = 'empc_motor';
open_system(mdl)
sim(mdl)



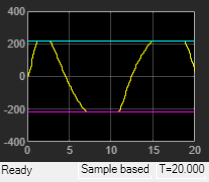
The closed-loop response is identical to the traditional MPC controller designed in DC Servomotor with Constraint on Unmeasured Output.
Control Using Sub-Optimal Explicit MPC
To reduce the memory footprint, you can use the simplify function to reduce the number of regions. For example, you can remove regions whose Chebyshev radius is smaller than 0.08. However, the price you pay is that the controller performance is suboptimal within those regions.
mpcobjExplicitSimplified = simplify(mpcobjExplicit,'radius',0.08)
Regions to analyze: 76/ 76 --> 37 regions deleted. Explicit MPC Controller --------------------------------------------- Controller sample time: 0.1 (seconds) Polyhedral regions: 39 Number of parameters: 6 Is solution simplified: Yes State Estimation: Default Kalman gain --------------------------------------------- Type 'mpcobjExplicitSimplified.MPC' for the original implicit MPC design. Type 'mpcobjExplicitSimplified.Range' for the valid range of parameters. Type 'mpcobjExplicitSimplified.OptimizationOptions' for the options used in multi-parametric QP computation. Type 'mpcobjExplicitSimplified.PiecewiseAffineSolution' for regions and gain in each solution.
The number of piecewise affine regions has been reduced.
Compare the closed-loop simulation results between suboptimal explicit MPC and explicit MPC.
[y3,t3,u3] = sim(mpcobjExplicitSimplified, Tf, r);
-->Converting model to discrete time. Assuming no disturbance added to measured output #1. -->"Model.Noise" is empty. Assuming white noise on each measured output.
The simulation results are not the same.
fprintf('Difference between exact and suboptimal explicit MPC trajectories = %g\n',... norm(u3-u2)+norm(y3-y2));
Difference between exact and suboptimal explicit MPC trajectories = 439.399
Plot results.
figure subplot(3,1,1) plot(t1,y1(:,1),t3,y3(:,1),'r:') grid title('Angle (rad)') legend('Explicit','sub-optimal Explicit') subplot(3,1,2) plot(t1,y1(:,2),t3,y3(:,2),'r:') grid title('Torque (Nm)') legend('Explicit','sub-optimal Explicit') subplot(3,1,3) plot(t1,u1,t3,u3,'r:') grid title('Voltage (V)') legend('Explicit','sub-optimal Explicit')

The simulation results show that the suboptimal explicit MPC performance is slightly worse than the performance of the explicit MPC.
References
[1] A. Bemporad and E. Mosca, "Fulfilling hard constraints in uncertain linear systems by reference managing," Automatica, vol. 34, no. 4, pp. 451-461, 1998.
bdclose(mdl)
See Also
Functions
generateExplicitMPC|generateExplicitRange|generateExplicitOptions|simplify|generatePlotParameters|plotSection|mpcmoveExplicit|sim
Objects
mpc|explicitMPC|mpcstate