Model Predictive Control of a Single-Input-Single-Output Plant

This example shows how to control a double integrator plant with input saturation in Simulink®.

Define the Plant Model

Define the plant model as a double integrator (the input is the manipulated variable and the output the measured output).

plant = tf(1,[1 0 0]);

Design the MPC Controller

Create the controller object with a sampling period of 0.1 seconds, a prediction horizon of 10 steps and a control horizon of and 3 moves.

mpcobj = mpc(plant, 0.1, 10, 3);

-->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000.
-->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000.
-->"Weights.OutputVariables" is empty. Assuming default 1.00000.

Because you have not specified the weights of the quadratic cost function to be minimized by the controller, their value is assumed to be the default one (0 for the manipulated variables, 0.1 for the manipulated variable rates, 1 for the output variables). Also, at this point the MPC problem is still unconstrained as you have not specified any constraint yet.

Specify actuator saturation limits as constraints on the manipulated variable.

mpcobj.MV = struct('Min',-1,'Max',1);

Simulate Using Simulink

Simulink is a graphical block diagram environment for multidomain system simulation. You can connect blocks representing dynamical systems (in this case the plant and the MPC controller) and simulate the closed loop.

% Check that Simulink is installed, otherwise display a message and return
if ~mpcchecktoolboxinstalled('simulink')
    disp('Simulink is required to run this example.')
    return
end

Open the pre-existing Simulink model for the closed-loop simulation. The plant model is implemented with two integrator blocks in series. The variable-step ode45 integration algorithm is used to calculate the continuous time loop behavior. The MPC Controller block is configured to use the workspace mpcobj object as controller. The manipulated variables and the output and reference signal. The output signal is also saved by the To-Workspace block.

mdl = 'mpc_doubleint';
open_system(mdl)

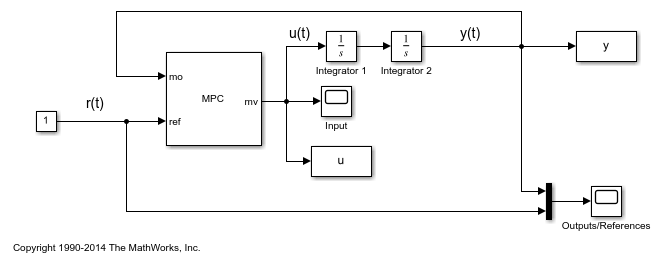
Simulate closed-loop control of the linear plant model in Simulink. Note that before the simulation starts the plant model in mpcobj is converted to a discrete state space model. By default, the controller uses as observer a Kalman filter designer assuming a white noise disturbance on each plant output.

sim(mdl)        % you can also simulate by pressing the "Run" button.

-->Converting the "Model.Plant" property to state-space.
-->Converting model to discrete time.
   Assuming no disturbance added to measured output #1.
-->"Model.Noise" is empty. Assuming white noise on each measured output.

The closed-loop response shows good setpoint tracking performance, as the plant output tracks its reference after about 2.5 seconds. As expected, the manipulated variable stays within the predefined constraints.

Close the open Simulink model without saving any change.

bdclose(mdl)