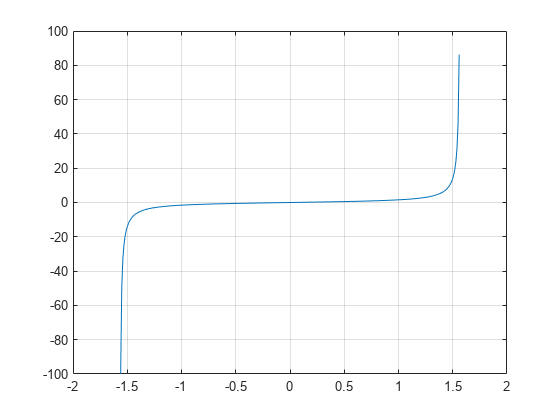
tan
Tangent of argument in radians
Syntax
Description
Examples
Input Arguments
Output Arguments
More About
Tips
In floating-point arithmetic,
tanis a bounded function. That is,tandoes not return values ofInfor-Infat points of divergence that are multiples ofpi, but a large magnitude number instead. This stems from the inaccuracy of the floating-point representation of π.