mean
Average or mean value of array
Syntax
Description
M = mean( returns the mean of the elements of
A)A along the first array dimension whose size does not equal
1.
If
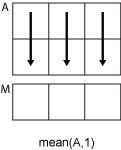
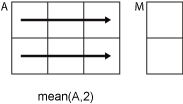
Ais a vector, thenmean(A)returns the mean of the elements.If
Ais a matrix, thenmean(A)returns a row vector containing the mean of each column.If
Ais a multidimensional array, thenmean(A)operates along the first array dimension whose size does not equal 1, treating the elements as vectors. The size ofMin this dimension becomes1, while the sizes of all other dimensions remain the same as inA.If
Ais a table or timetable, thenmean(A)returns a one-row table containing the mean of each variable. (since R2023a)
M = mean(___, returns the mean with a
specified data type for any of the previous syntaxes. outtype)outtype can be
"default", "double", or "native".
M = mean(___, specifies whether to
include or omit missing values in missingflag)A. For example,
mean(A,"omitmissing") ignores all missing values when computing the mean. By
default, mean includes missing values.
M = mean(___,Weights= specifies a weighting
scheme W)W and returns the weighted mean. (since R2024a)