allcycles
Description
[
also returns the edges in each cycle. The output cycles,edgecycles] = allcycles(G)edgecycles is a cell
array where edgecycles{k} gives the edges in the corresponding cycle,
cycles{k}.
[___] = allcycles(
specifies additional options using one or more name-value arguments. You can use any of the
output argument combinations in previous syntaxes. For example, you can specify
G,Name,Value)MaxNumCycles and a scalar to limit the number of cycles
returned.
Examples
Create a directed graph with nine nodes. Plot the graph.
s = [1 2 3 6 5 5 4 6 9 8 8 7]; t = [2 3 6 5 2 4 1 9 8 5 7 4]; G = digraph(s,t); plot(G)

Calculate all cycles in the graph.
cycles = allcycles(G)
cycles=5×1 cell array
{[ 1 2 3 6 5 4]}
{[1 2 3 6 9 8 5 4]}
{[1 2 3 6 9 8 7 4]}
{[ 2 3 6 5]}
{[ 2 3 6 9 8 5]}
The second output argument of allcycles returns the edges that are contained in each cycle. This is particularly useful for multigraphs, where the edge index is required to uniquely identify the edges in each cycle.
Create a directed multigraph with eight nodes and 18 edges. Specify names for the nodes. Plot the graph with labeled nodes and edges.
s = [1 1 2 2 3 3 2 2 4 6 8 6 6 7 3 3 5 3];
t = [2 3 1 3 2 1 4 4 6 2 6 7 8 8 5 5 7 7];
names = {'A','B','C','D','E','F','G','H'};
G = digraph(s,t,[],names);
p = plot(G,'EdgeLabel',1:numedges(G));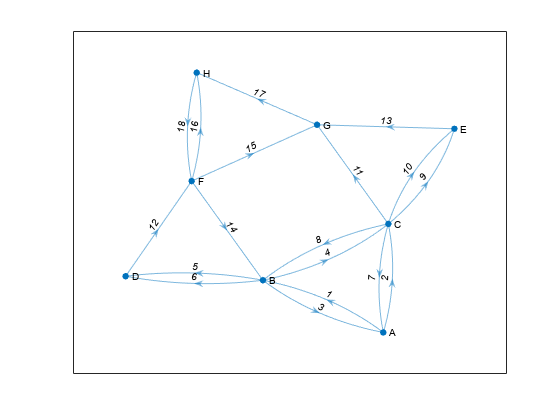
Calculate all cycles in the graph. Specify two output arguments to also return the edge indices for edges in each cycle.
[cycles,edgecycles] = allcycles(G);
View the nodes and edges in the fifth cycle.
cycles{5}ans = 1×7 cell
{'A'} {'C'} {'E'} {'G'} {'H'} {'F'} {'B'}
edgecycles{5}ans = 1×7
2 9 13 17 18 14 3
Highlight the nodes and edges in the fifth cycle.
highlight(p,'Edges',edgecycles{5},'EdgeColor','r','LineWidth',1.5,'NodeColor','r','MarkerSize',6)

Use the 'MaxNumCycles', 'MaxCycleLength', and 'MinCycleLength' options to limit the number of cycles returned by allcycles.
Create an adjacency matrix for a complete graph with 20 nodes. Create an undirected graph from the adjacency matrix, omitting self-loops.
A = ones(20);
G = graph(A,'omitselfloops');Since all of the nodes in the graph are connected to all other nodes, there are a large number of cycles in the graph (more than 1.7e17). Therefore, it is not feasible to calculate all of the cycles since the results will not fit in memory. Instead, calculate the first 10 cycles.
cycles1 = allcycles(G,'MaxNumCycles',10)cycles1=10×1 cell array
{[ 1 2 3]}
{[ 1 2 3 4]}
{[ 1 2 3 4 5]}
{[ 1 2 3 4 5 6]}
{[ 1 2 3 4 5 6 7]}
{[ 1 2 3 4 5 6 7 8]}
{[ 1 2 3 4 5 6 7 8 9]}
{[ 1 2 3 4 5 6 7 8 9 10]}
{[ 1 2 3 4 5 6 7 8 9 10 11]}
{[1 2 3 4 5 6 7 8 9 10 11 12]}
Now calculate the first 10 cycles that have a cycle length less than or equal to 3.
cycles2 = allcycles(G,'MaxNumCycles',10,'MaxCycleLength',3)
cycles2=10×1 cell array
{[ 1 2 3]}
{[ 1 2 4]}
{[ 1 2 5]}
{[ 1 2 6]}
{[ 1 2 7]}
{[ 1 2 8]}
{[ 1 2 9]}
{[1 2 10]}
{[1 2 11]}
{[1 2 12]}
Finally, calculate the first 10 cycles that have a cycle length greater than or equal to 4.
cycles3 = allcycles(G,'MaxNumCycles',10,'MinCycleLength',4)
cycles3=10×1 cell array
{[ 1 2 3 4]}
{[ 1 2 3 4 5]}
{[ 1 2 3 4 5 6]}
{[ 1 2 3 4 5 6 7]}
{[ 1 2 3 4 5 6 7 8]}
{[ 1 2 3 4 5 6 7 8 9]}
{[ 1 2 3 4 5 6 7 8 9 10]}
{[ 1 2 3 4 5 6 7 8 9 10 11]}
{[ 1 2 3 4 5 6 7 8 9 10 11 12]}
{[1 2 3 4 5 6 7 8 9 10 11 12 13]}
Examine how the outputs of the cyclebasis and allcycles functions scale with the number of edges in a graph.
Create and plot a square grid graph with three nodes on each side of the square.
n = 5; A = delsq(numgrid('S',n)); G = graph(A,'omitselfloops'); plot(G)
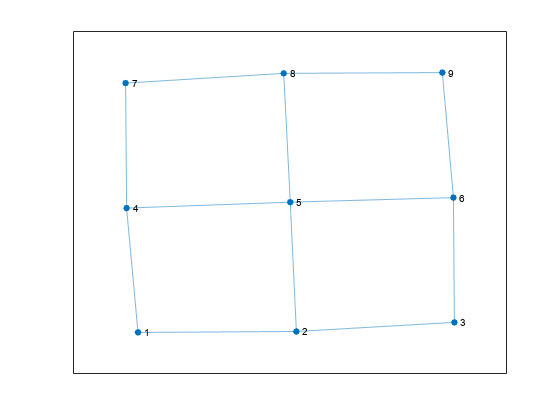
Compute all cycles in the graph using allcycles. Use the tiledlayout function to construct an array of subplots and highlight each cycle in a subplot. The results indicate there are a total of 13 cycles in the graph.
[cycles,edgecycles] = allcycles(G); tiledlayout flow for k = 1:length(cycles) nexttile highlight(plot(G),cycles{k},'Edges',edgecycles{k},'EdgeColor','r','NodeColor','r') title("Cycle " + k) end

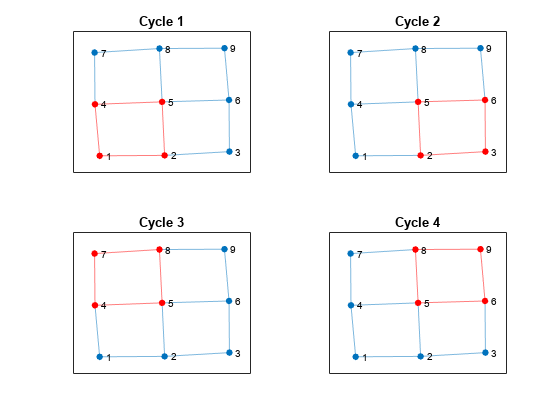
Some of these cycles can be seen as combinations of smaller cycles. The cyclebasis function returns a subset of the cycles that form a basis for all other cycles in the graph. Use cyclebasis to compute the fundamental cycle basis and highlight each fundamental cycle in a subplot. Even though there are 13 cycles in the graph, there are only four fundamental cycles.
[cycles,edgecycles] = cyclebasis(G); tiledlayout flow for k = 1:length(cycles) nexttile highlight(plot(G),cycles{k},'Edges',edgecycles{k},'EdgeColor','r','NodeColor','r') title("Cycle " + k) end
Now, increase the number of nodes on each side of the square graph from three to four. This represents a small increase in the size of the graph.
n = 6; A = delsq(numgrid('S',n)); G = graph(A,'omitselfloops'); figure plot(G)
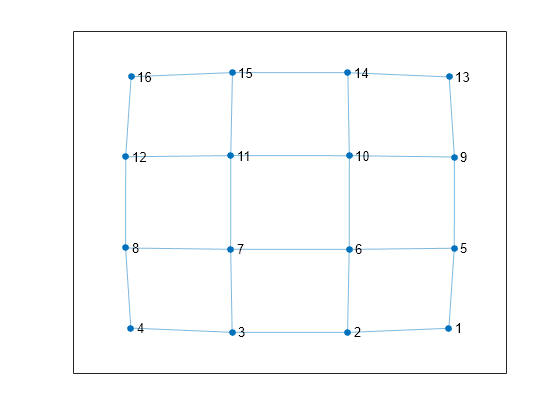
Use allcycles to compute all of the cycles in the new graph. For this graph there are over 200 cycles, which is too many to plot.
allcycles(G)
ans=213×1 cell array
{[ 1 2 3 4 8 7 6 5]}
{[ 1 2 3 4 8 7 6 10 9 5]}
{[1 2 3 4 8 7 6 10 11 12 16 15 14 13 9 5]}
{[ 1 2 3 4 8 7 6 10 11 15 14 13 9 5]}
{[ 1 2 3 4 8 7 6 10 14 13 9 5]}
{[ 1 2 3 4 8 7 11 10 6 5]}
{[ 1 2 3 4 8 7 11 10 9 5]}
{[ 1 2 3 4 8 7 11 10 14 13 9 5]}
{[ 1 2 3 4 8 7 11 12 16 15 14 10 6 5]}
{[ 1 2 3 4 8 7 11 12 16 15 14 10 9 5]}
{[ 1 2 3 4 8 7 11 12 16 15 14 13 9 5]}
{[1 2 3 4 8 7 11 12 16 15 14 13 9 10 6 5]}
{[ 1 2 3 4 8 7 11 15 14 10 6 5]}
{[ 1 2 3 4 8 7 11 15 14 10 9 5]}
{[ 1 2 3 4 8 7 11 15 14 13 9 5]}
{[ 1 2 3 4 8 7 11 15 14 13 9 10 6 5]}
⋮
Despite the large number of cycles in the graph, cyclebasis still returns a small number of fundamental cycles. Each of the cycles in the graph can be constructed using only nine fundamental cycles.
[cycles,edgecycles] = cyclebasis(G); figure tiledlayout flow for k = 1:length(cycles) nexttile highlight(plot(G),cycles{k},'Edges',edgecycles{k},'EdgeColor','r','NodeColor','r') title("Cycle " + k) end

The large increase in the number of cycles with only a small change in the size of the graph is typical for some graph structures. The number of cycles returned by allcycles can grow exponentially with the number of edges in the graph. However, the number of cycles returned by cyclebasis can, at most, grow linearly with the number of edges in the graph.
Input Arguments
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: allcycles(G,'MaxNumCycles',100) returns only the first 100
cycles in the graph.
Maximum number of cycles, specified as the comma-separated pair consisting of
'MaxNumCycles' and a nonnegative integer scalar. This option is
useful when the number of cycles in a graph grows large enough to hit memory limits.
You can specify MaxNumCycles to limit the number of cycles returned
by allcycles so that the results fit within available
memory.
Example: allcycles(G,'MaxNumCycles',100)
Maximum cycle length, specified as the comma-separated pair consisting of
'MaxCycleLength' and a positive integer scalar. This option
filters the results returned by allcycles so that no cycles with
length larger than the specified limit are returned. The length of a cycle is measured
by the number of edges in it, ignoring edge weights.
To find cycles with a range of lengths, specify both
'MaxCycleLength' and 'MinCycleLength'. To find
cycles with an exact specified length, specify the same value for both
'MaxCycleLength' and 'MinCycleLength'.
Example: allcycles(G,'MaxCycleLength',4) returns cycles that
have a length less than or equal to 4.
Example: allcycles(G,'MinCycleLength',3,'MaxCycleLength',5)
returns cycles that have a length of 3, 4, or 5.
Minimum cycle length, specified as the comma-separated pair consisting of
'MinCycleLength' and a positive integer scalar. This option
filters the results returned by allcycles so that no cycles with
length smaller than the specified limit are returned. The length of a cycle is
measured by the number of edges in it, ignoring edge weights.
To find cycles with a range of lengths, specify both
'MaxCycleLength' and 'MinCycleLength'. To find
cycles with an exact specified length, specify the same value for both
'MaxCycleLength' and 'MinCycleLength'.
Example: allcycles(G,'MinCycleLength',2) returns cycles that
have a length greater than or equal to 2.
Example: allcycles(G,'MinCycleLength',3,'MaxCycleLength',5)
returns cycles that have a length of 3, 4, or 5.
Output Arguments
Graph cycles, returned as a cell array. Each element cycles{k}
contains the nodes that belong to one of the cycles in G. Each cycle
begins with the node that has the smallest node index, and the cycles are returned in
lexicographical order. Cycles in undirected graphs are returned only once, following a
single direction. If G does not contain any cycles, then
cycles is empty.
The data type of the cells in cycles depends on whether the input
graph contains node names:
If graph
Gdoes not have node names, then each elementcycles{k}is a numeric vector of node indices.If graph
Ghas node names, then each elementcycles{k}is a cell array of character vector node names.
Edges in each cycle, returned as a cell array. Each element
edgecycles{k} contains the edge indices for edges in the
corresponding cycle, cycles{k}. If G does not
contain any cycles, then edgecycles is empty.
More About
A cycle exists in a graph when there is a nonempty path in which only the
first and last nodes are repeated. That is, aside from the first node being repeated
at the end of the path to close the cycle, no other nodes are repeated. An example
of a cycle is: (Node1 - Node2 - Node3 - Node1). By convention,
allcycles does not return the last node in the cycle
since it is the same as the first.
A cycle cannot traverse the same edge twice. For example, the cycle (Node1 - Node2 - Node1) in an undirected graph only exists if there is more than one edge connecting Node1 and Node2. By this definition, self-loops count as cycles, though they cannot be part of a larger cycle.
Tips
The number of cycles in a graph depends heavily on the structure of the graph. For some graph structures, the number of cycles can grow exponentially with the number of nodes. For example, a complete graph with 12 nodes given by
G = graph(ones(12))contains nearly 60 million cycles. Use theMaxNumCycles,MaxCycleLength, andMinCycleLengthoptions to control the output ofallcyclesin these cases.
Version History
Introduced in R2021a
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)