2-D Fourier Transforms
The fft2 function transforms
2-D data into frequency space. For example, you can transform a 2-D
optical mask to reveal its diffraction pattern.
Two-Dimensional Fourier Transform
The following formula defines the discrete Fourier transform Y of an m-by-n matrix X.
ωm and ωn are complex roots of unity defined by the following equations.
i is the imaginary unit, p and j are indices that run from 0 to m–1, and q and k are indices that run from 0 to n–1. The indices for X and Y are shifted by 1 in this formula to reflect matrix indices in MATLAB®.
Computing the 2-D Fourier transform of X is
equivalent to first computing the 1-D transform of each column of X,
and then taking the 1-D transform of each row of the result. In other
words, the command fft2(X) is equivalent to Y
= fft(fft(X).').'.
2-D Diffraction Pattern
In optics, the Fourier transform can be used to describe the diffraction pattern produced by a plane wave incident on an optical mask with a small aperture [1]. This example uses the fft2 function on an optical mask to compute its diffraction pattern.
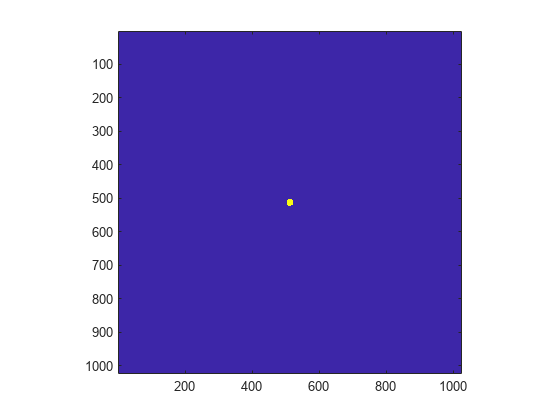
Create a logical array that defines an optical mask with a small, circular aperture.
n = 2^10; % size of mask M = zeros(n); I = 1:n; x = I-n/2; % mask x-coordinates y = n/2-I; % mask y-coordinates [X,Y] = meshgrid(x,y); % create 2-D mask grid R = 10; % aperture radius A = (X.^2 + Y.^2 <= R^2); % circular aperture of radius R M(A) = 1; % set mask elements inside aperture to 1 imagesc(M) % plot mask axis image
Use fft2 to compute the 2-D Fourier transform of the mask, and use the fftshift function to rearrange the output so that the zero-frequency component is at the center. Plot the resulting diffraction pattern frequencies. Blue indicates small amplitudes and yellow indicates large amplitudes.
DP = fftshift(fft2(M));
imagesc(abs(DP))
axis image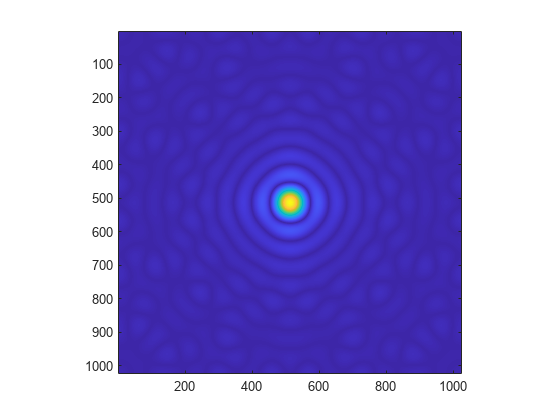
To enhance the details of regions with small amplitudes, plot the 2-D logarithm of the diffraction pattern. Very small amplitudes are affected by numerical round-off error, and the rectangular grid causes radial asymmetry.
imagesc(abs(log2(DP)))
axis image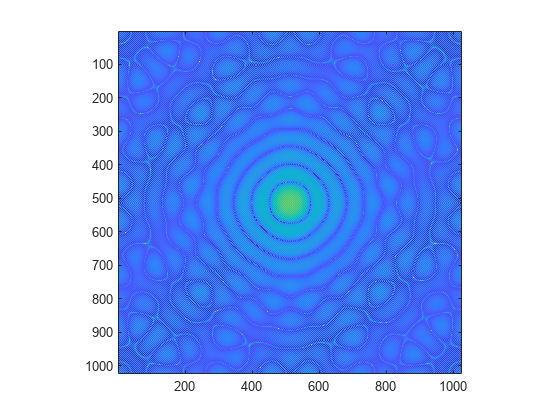
For information on Fourier transform representation of 2-D images, see Fast Fourier Transform (Image Processing Toolbox).
References
[1] Fowles, G. R. Introduction to Modern Optics. New York: Dover, 1989.
See Also
fft2 | fftshift | fftn | ifft2 | fft