braun
Braun Perspective Cylindrical Projection
Classification
Cylindrical
Identifier
braun
Graticule
Meridians: Equally spaced straight parallel lines.
Parallels: Unequally spaced straight parallel lines, perpendicular to the meridians. Spacing increases toward the poles.
Poles: Straight lines equal in length to the Equator.
Symmetry: About any meridian or the Equator.
Features
This is an perspective projection from a point on the Equator opposite a given meridian onto a cylinder secant at standard parallels. It is not equal-area, equidistant, or conformal. Scale is true along the standard parallels and constant between two parallels equidistant from the Equator. There is no distortion along the standard parallels, but it increases moderately away from these parallels, becoming severe at the poles.
Parallels
For cylindrical projections, only one standard parallel is specified. The other standard parallel is the same latitude with the opposite sign. For this projection, any latitude may be chosen; the default is arbitrarily set to 0º.
Remarks
This projection was first described by Braun in 1867. It is less well known than the specific forms of it called the Gall Stereographic and the Bolshoi Sovietskii Atlas Mira projections.
This implementation of the Braun perspective cylindrical projection is applicable only for coordinates that are referenced to a sphere.
Example
landareas = shaperead('landareas.shp','UseGeoCoords',true);
axesm ('braun', 'Frame', 'on', 'Grid', 'on');
geoshow(landareas,'FaceColor',[1 1 .5],'EdgeColor',[.6 .6 .6]);
tissot;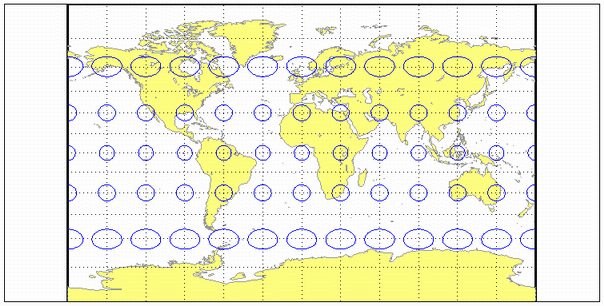
Version History
Introduced before R2006a