HDL Implementation of Variable-Size FFT
This example shows how to implement a variable-size FFT by using a single FFT core.
This example includes two models VariableSizeFFTHDLExample and VariableSizeFFTArbitraryValidPatternHDLExample that show variable-size FFT implementations for different input valid patterns.
Many popular standards like WLAN, WiMax, digital video broadcast (DVB), digital audio broadcast (DAB), and long term evolution (LTE) provide multiple bandwidth options. The required FFT length for OFDM modulation and demodulation for these standards varies with bandwidth option. For example, LTE supports different channel bandwidth options from 1.4 MHz to 20 MHz, which require FFT lengths of 128 to 2048 respectively. The FFT block generates HDL code for a specific FFT length. This example demonstrates how to use the FFT block to implement a variable-size FFT.
This example generates input data in MATLAB® and imports it to Simulink® for the simulation. The imported data is fed to the implementations of variable-size FFT using a single FFT and multiple FFTs. To demonstrate that the single-FFT implementation matches the results of using multiple FFTs of various sizes, both the output streams from the Simulink simulation are exported to MATLAB and compared.
Model Architecture
The top-level subsystem in both the models implement a variable-size FFT. The top subsystem uses a single FFT block and the bottom subsystem provides reference data by using multiple FFT blocks of various sizes.
The model VariableSizeFFTHDLExample can process data with a gap between valid samples, provided the gap depends on FFT length.
modelname = 'VariableSizeFFTHDLExample';
open_system(modelname);

Configuration of FFT Lengths
The FFT lengths are specified through a variable fftLenVecMulFFTs. The largest of these lengths is stored in a variable fftLenSinFFT and used as the FFT length for the FFT block in the 'Variable Size FFT using Single FFT' subsystem.
The input fftLenIn is generated by using the vector of FFT lengths specified in fftLenVecMulFFTs.
fftLenVecMulFFTs = [128;256;512;1024;2048]; % Single FFT length used by variable size FFT. fftLenSinFFT = max(fftLenVecMulFFTs); % Generate |fftLenIn| by repeating each element of |fftLenVecMulFFTs| by % |fftLenSinFFT| times and arranging in a single column. fflen =repmat(fftLenVecMulFFTs.',fftLenSinFFT,1); fftLenIn = uint16(fflen(:));
Input Generation
dataIn, validIn, and fftLenIn inputs are generated in MATLAB and imported to the Simulink model. Random complex input data randInputData is generated for each of the FFT lengths specified in fftLenVecMulFFTs. Different FFT lengths correspond to different bandwidths and different sampling rates. For instance, in LTE, the FFT lengths of 128, 256, 512, 1024, and 2048 correspond to the sampling rates 1.92 MHz, 3.84 MHz, 7.68 MHz, 15.36 MHz, and 30.72 MHz respectively. The symbol time for any FFT length is 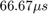 . The example operates at the highest rate among the FFT lengths specified.
. The example operates at the highest rate among the FFT lengths specified.
The dataIn signal is generated by padding zeros in between the randInputData samples. The figure below shows the input data and valid patterns for fftLenVecMulFFTs of 256 and 512 and fftLenSinFFT being 2048. For the FFT length of 256, the example inserts 7 invalid samples for every valid sample and for the FFT length of 512, the code inserts 3 invalid samples for every valid sample.
The model VariableSizeFFTHDLExample requires the input valid pattern to have a gap between valid samples as shown in the figure below.

rng('default'); dataIn = zeros(length(fftLenVecMulFFTs)*fftLenSinFFT,1); validIn = false(length(fftLenVecMulFFTs)*fftLenSinFFT,1); % Loop over the FFT lengths for ind = 1:length(fftLenVecMulFFTs) % Generate data of FFT length samples randInputData = complex(randn(1,fftLenVecMulFFTs(ind)),randn(1,fftLenVecMulFFTs(ind))); % Zero padding in between input data samples upSamplingFac = fftLenSinFFT/fftLenVecMulFFTs(ind); dataIn((ind-1)*fftLenSinFFT+1:fftLenSinFFT*ind) = upsample(randInputData,upSamplingFac); % Valid corresponding to the generated data tempValid = true(1,fftLenVecMulFFTs(ind)); validIn((ind-1)*fftLenSinFFT+1:fftLenSinFFT*ind) = upsample(tempValid,upSamplingFac); end inputDataType = 'fixdt(1,16,14)'; % Input data type can be modified here set_param('VariableSizeFFTHDLExample/Data Type Conversion','OutDataTypeStr', inputDataType); % Get FFT latency fftObj = dsp.HDLFFT('FFTLength',fftLenSinFFT,... 'Architecture','Streaming Radix 2^2',... 'ComplexMultiplication','Use 3 multipliers and 5 adders',... 'BitReversedOutput',false,... 'BitReversedInput',false,... 'Normalize',false); latency=getLatency(fftObj); % Default latency is 4137 for 2048 point FFT. additionPipelineDelay = 6; % Number of additional pipeline delays % Simulink simulation end time Total Latency = Latency of FFT + Latency of % data controller (5 clock cycles). % Total simulation running time = Total % number of input samples + Total Latency + Pipeline delay. simTime = fftLenSinFFT*(length(fftLenVecMulFFTs) + 1) + latency + additionPipelineDelay ;
Variable-Size FFT Using Single FFT
The 'Variable-Size FFT using Single FFT' design includes a Data Controller, an FFT block, and a Bin selection subsystem.
open_system([modelname '/Variable Size FFT using Single FFT']);

The Data Controller subsystem controls the input data so that the input to the FFT block has data samples with zeros padded in between them. The FFT block is configured for an FFT length of 2048, the largest FFT length required by the LTE standard. To simplify selection of the output bins, the FFT block is configured to output the samples in bit-natural order. The FFT length is specified through input port and is sampled at the start of the frame. The requested FFT length must be delayed to match the FFT latency. The FFT length is registered using the start output signal of the FFT and the generated end of the frame signal. This method avoids implementing a large delay-matching memory. Since the input data has zeros in between samples, the output of the large FFT contains repeated copies of the FFT length samples. To get the required FFT output, the first FFT length samples are collected from the FFT output. This operation is performed by modifying the output valid signal of the FFT using the Bin selection subsystem.
Multiple FFTs for Reference
This subsystem is used as a reference to compare against the output of Variable Size FFT using Single FFT. The subsystem includes five different FFT blocks (FFT 128, FFT 256, FFT 512, FFT 1024, and FFT 2048) and one MATLAB Function block. The input data will be fed to all five FFTs. Depending on the requested FFT length, one of the five FFT blocks is activated and FFT operation is performed. The MATLAB function block pickFFTData selects the output from the appropriate FFT block. The output is saved to MATLAB for comparison with the output of the Variable-Size FFT using Single FFT.
open_system([modelname '/Multiple FFTs for Reference']);

Run Simulink Model
The MATLAB script configures desired vector of FFT lengths, the size of the single FFT, and generates input data with a valid signal. It then runs the model, and compares the output of the two subsystems in MATLAB.
Run the model using the sim command on the MATLAB command line.
sim(modelname);
Verification
The output from both subsystems is sent to the MATLAB workspace and the difference is plotted. In this case, the output of the two subsystems are identical and the error between the two sets of values is 0.
dataOut1 = out1(:); dataOut2 = out2(:); figVSF = figure('Visible', 'off'); plot(abs(dataOut1-dataOut2)); title('Difference between the two outputs for fixed valid pattern') xlabel('Sample Index'); ylabel('Error'); figVSF.Visible = 'on'; bdclose(modelname);

Support for Arbitrary Input Valid Patterns
The above model VariableSizeFFTHDLExample has a requirement of having a minimum gap between input data samples. The gap depends on the specified FFT length and the largest FFT length handled by the design. There may be cases where the input data may not conform to this pattern. For example, the data may be continuous and padded with zeros at the end of the input data samples. The following figure shows a contiguous input valid pattern with invalid samples padded at the end of input data samples for FFT lengths of 256 and 512. The single FFT length is set to 2048. In this case, the 256 valid samples are followed by 1792 invalid samples and the 512 valid samples are followed by 1536 invalid samples.

In such scenario, the design has to store the input samples into a RAM, and pad invalid samples between valid samples before sending it on to the FFT. The model VariableSizeFFTArbitraryValidPatternHDLExample can handle any arbitrary pattern of valid input so long as the gap between frames is at least the single FFT length (2048 samples for LTE). This model is the same as the model VariableSizeFFTHDLExample, except for the data controller subsystem. The data controller subsystem in the model uses a RAM of size 2*fftLenSinFFT (as shown in the figure below) to store input samples, reads out the valid samples while padding zeros between them and then passing them to the FFT. While the input data is being written into one half of the memory, the data is read from the other half of the memory. As a result, the total latency is increased by fftLenSinFFT.
modelname = 'VariableSizeFFTArbitraryValidPatternHDLExample'; load_system(modelname); open_system([modelname '/Variable Size FFT using Single FFT/Data Controller']);

Arbitrary Input Data and Valid Generation
For generating arbitrary data and valid inputs, users can select any of these three options: zero padding of fixed size in between data samples, zero padding at the end of data samples, and zero padding of random size in between data samples. The input data and valid generation for these three different zero padding patterns are shown below. The VariableSizeFFTArbitraryValidPatternHDLExample model uses the generated data and valid for simulation and verification.
% Initialization of input data and valid dataIn = zeros(length(fftLenVecMulFFTs)*fftLenSinFFT,1); validIn = false(length(fftLenVecMulFFTs)*fftLenSinFFT,1); zeroPaddingPattern = 'InBetween'; %'AtEnd','Random' switch zeroPaddingPattern case 'InBetween' % Zero padding in between input data samples for ind = 1:length(fftLenVecMulFFTs) % Generate data of FFT length samples randInputData = complex(randn(1,fftLenVecMulFFTs(ind)),randn(1,fftLenVecMulFFTs(ind))); % Zero padding in between input data samples upSamplingFac = fftLenSinFFT/fftLenVecMulFFTs(ind); dataIn((ind-1)*fftLenSinFFT+1:fftLenSinFFT*ind) = upsample(randInputData,upSamplingFac); % Valid corresponding to the generated data validIn((ind-1)*fftLenSinFFT+1:upSamplingFac:fftLenSinFFT*ind) = true; end case 'AtEnd' % Zero padding at the end of input data samples for ind = 1:length(fftLenVecMulFFTs) % Generate data of FFT length samples randInputData = complex(randn(1,fftLenVecMulFFTs(ind)),randn(1,fftLenVecMulFFTs(ind))); % Zero padded data dataIn(((ind-1)*fftLenSinFFT+1):((ind-1)*fftLenSinFFT+fftLenVecMulFFTs(ind))) = randInputData; % Valid corresponding to data generated validIn(((ind-1)*fftLenSinFFT+1):((ind-1)*fftLenSinFFT+fftLenVecMulFFTs(ind))) = true; end otherwise % Random for ind =1:length(fftLenVecMulFFTs) % Zero padding at random randIndices = randperm(fftLenSinFFT); % Generate data of FFT length samples randInputData = complex(randn(1,fftLenVecMulFFTs(ind)),randn(1,fftLenVecMulFFTs(ind))); indices = randIndices(1:fftLenVecMulFFTs(ind)); % If the random indices does not have the first sample if(sum(indices==1)==0) indices(1) = 1; end % Zero padded data dataIn(indices+(ind-1)*fftLenSinFFT) = randInputData; % Valid corresponding to data generated validIn(indices+(ind-1)*fftLenSinFFT) = true; end end
Run the Simulink model
Before running the model, make sure that dataIn, validIn, fftLenIn, and the necessary variables are initialized.
sim(modelname);
Verification
dataOut1 = out1(:); dataOut2 = out2(:); figVSFAIV = figure('Visible', 'off'); plot(abs(dataOut1-dataOut2)); title('Difference between the two outputs for arbitrary valid pattern') xlabel('Sample Index'); ylabel('Error'); figVSFAIV.Visible = 'on'; bdclose(modelname);

HDL Code Generation and Verification
To generate the HDL code referenced in this example, an HDL Coder™ license is needed.
You can use the commands makehdl and makehdltb to generate the HDL code and the testbench for the subsystems.
HDL code generated for the Variable Size FFT subsystems were synthesized for the Xilinx® Zynq®-7000 ZC706 board. The synthesis results are shown in the following table.
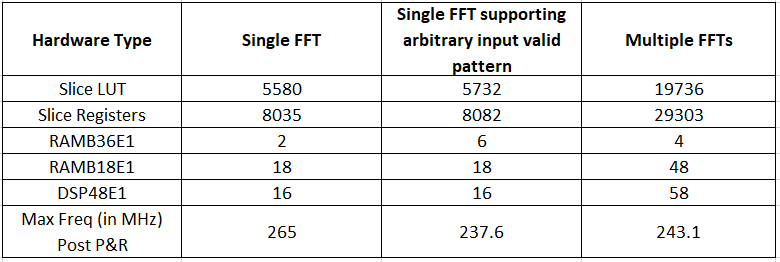
The table above shows that implementing a variable-size FFT using a single FFT uses fewer hardware resources than using a multiple FFT solution. To support an arbitrary input valid pattern, the hardware implementation uses more RAM.