Online Recursive Least Squares Estimation

This example uses:

This example shows how to implement an online recursive least squares estimator. You estimate a nonlinear model of an internal combustion engine and use recursive least squares to detect changes in engine inertia.

Engine Model

The engine model includes nonlinear elements for the throttle and manifold system, and the combustion system. The model input is the throttle angle and the model output is the engine speed in rpm.

open_system('iddemo_engine');
sim('iddemo_engine')

The engine model is set up with a pulse train driving the throttle angle from open to closed. The engine response is nonlinear, specifically the engine rpm response time when the throttle is open and closed is different.

At 100 seconds into the simulation an engine fault occurs causing the engine inertia to increase (the engine inertia, J, is modeled in the iddemo_engine/Vehicle Dynamics block). The inertia change causes engine response times at open and closed throttle positions to increase. You use online recursive least squares to detect the inertia change.

open_system('iddemo_engine/trpm')

Estimation Model

The engine model is a damped second order system with input and output nonlinearities to account for different response times at different throttle positions. Use the recursive least squares block to identify the following discrete system that models the engine:

$y_n = a_1 u_{n-1} + a_2 u_{n-1}^2 + a_3 y_{n-1}$

Since the estimation model does not explicitly include inertia we expect the $a$ values to change as the inertia changes. We use the changing $a$ values to detect the inertia change.

The engine has significant bandwidth up to 16Hz. Set the estimator sampling frequency to 2*160Hz or a sample time of 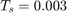$T_s = 0.003$ seconds.

Recursive Least Squares Estimator Block Setup

The 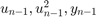$u_{n-1}, u_{n-1}^2, y_{n-1}$ terms in the estimated model are the model regressors and inputs to the recursive least squares block that estimates the $a$ values. You can implement the regressors as shown in the iddemo_engine/Regressors block.

open_system('iddemo_engine/Regressors');

Configure the Recursive Least Squares Estimator block:

Initial Estimate: None. By default, the software uses a value of 1.

Number of parameters: 3, one for each regressor coefficient.

Parameter Covariance Matrix: 1, the amount of uncertainty in initial guess of 1. Concretely, treat the estimated parameters as a random variable with variance 1.

Sample Time: .

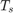Click Algorithm and Block Options to set the estimation options:

Estimation Method: Forgetting Factor

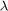Forgetting Factor: 1-2e-4. Since the estimated values are expected to change with the inertia, set the forgetting factor to a value less than 1. Choose $\lambda$ = 1-2e-4 which corresponds to a memory time constant of $T_0 = \frac{T_s}{1-\lambda}$ or 15 seconds. A 15 second memory time ensures that significant data from both the open and closed throttle position are used for estimation as the position is changed every 10 seconds.

Select the Output estimation error check box. You use this block output to validate the estimation.

Select the Output parameter covariance matrix check box. You use this block output to validate the estimation.

Clear the Add enable port check box.

External reset: None.

Validating the Estimated Model

The Error output of the Recursive Least Squares Estimator block gives the one-step-ahead error for the estimated model. This error is less than 5% indicating that for one-step-ahead prediction the estimated model is accurate.

open_system('iddemo_engine/Error (%)')

The diagonal of the parameter covariances matrix gives the variances for the $a_n$ parameters. The $a_3$ variance is small relative to the parameter value indicating good confidence in the estimated value. In contrast, the $a_1, a_2$ variances are large relative to the parameter values indicating a low confidence in these values.

While the small estimation error and covariances give confidence that the model is being estimated correctly, it is limited in that the error is a one-step-ahead predictor. A more rigorous check is to use the estimated model in a simulation model and compare with the actual model output. The Estimated Model section of the Simulink® model implements this.

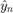The Regressors1 block is identical to the Regressors block use in the recursive estimator. The only difference is that the y signal is not measured from the plant but fed back from the output of the estimated model. The Output of the regressors block is multiplied by estimated $a_n$ values to give $\hat{y}_n$ an estimate of the engine speed.

open_system('iddemo_engine/trpm Est')

The estimated model output matches the model output fairly well. The steady-state values are close and the transient behavior is slightly different but not significantly so. Note that after 100 seconds when the engine inertia changes the estimated model output differs slightly more from the model output. This implies that the chosen regressors cannot capture the behavior of the model as well after the inertia change. This also suggests a change in system behavior.

The estimated model output combined with the low one-step-ahead error and parameter covariances gives us confidence in the recursive estimator.

Detecting Changes in Engine Inertia

The engine model is setup to introduce an inertia change 100 seconds into the simulation. The recursive estimator can be used to detect the change in inertia.

The recursive estimator takes around 50 seconds to converge to an initial set of parameter values. To detect the inertia change we examine the 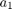$a_1$ model coefficient that influences the 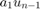$a_1 u_{n-1}$ term of the estimated model.

open_system('iddemo_engine/Detect Inertia Change')

The covariance for 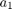$a_1$ , 0.05562, is large relative to the parameter value 0.1246 indicating low confidence in the estimated value. The time plot of 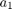$a_1$ shows why the covariance is large. Specifically 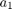$a_1$ is varying as the throttle position varies indicating that the estimated model is not rich enough to fully capture different rise times at different throttle positions and needs to adjust 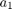$a_1$ . However, we can use this to identify the inertia changes as the average value of 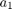$a_1$ changes as the inertia changes. You can use a threshold detector on the moving average of the 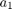$a_1$ parameter to detect changes in the engine inertia.

bdclose('iddemo_engine')