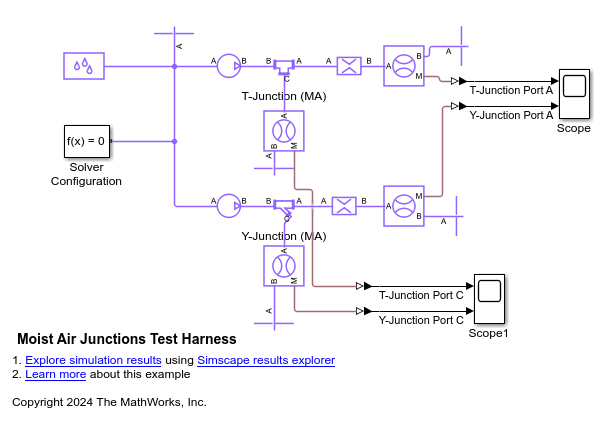
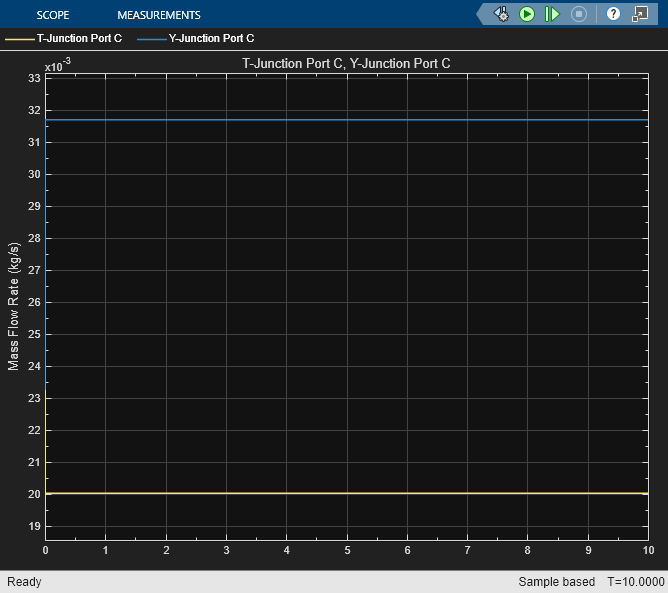
Y-Junction (MA)

Y-junction in a moist air network

Since R2024b

Libraries:
Simscape / Fluids / Moist Air / Pipes & Fittings

Description

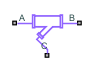
The Y-Junction (MA) block models a Y-junction consisting of a main branch and a side branch in a moist air network. The path between ports A and B is the main branch. The path between ports A and C or between ports B and C is the side branch. The side branch extends from the main branch at an angle specified by the value of the Junction angle between (A-C) parameter.

Flow Direction

The flow is converging when the flow through port C merges into the main flow. The flow is diverging when the branch flow splits from the main flow.

The block uses mode charts to determine each loss coefficient for a given flow configuration. This table describes the conditions and coefficients when the Loss coefficient model parameter is Custom.

Flow Scenario	ṁ_A	ṁ_B	ṁ_C	K_A	K_B	K_C
Stagnant	–	–	–	1 or last valid value	1 or last valid value	1 or last valid value
Diverging from node A	>ṁ_thresh	<-ṁ_thresh	<-ṁ_thresh	0	K_main,div	K_side,div
Diverging from node B	<-ṁ_thresh	>ṁ_thresh	<-ṁ_thresh	K_main,div	0	K_side,div
Converging to node A	<-ṁ_thresh	>ṁ_thresh	>ṁ_thresh	0	K_main,conv	K_side,conv
Converging to node B	>ṁ_thresh	<-ṁ_thresh	>ṁ_thresh	K_main,conv	0	K_side,conv
Converging to node C (branch)	>ṁ_thresh	>ṁ_thresh	<-ṁ_thresh	(K_main,conv + K_side,conv)/2	(K_main,conv + K_side,conv)/2	0
Diverging from node C (branch)	<-ṁ_thresh	<-ṁ_thresh	>ṁ_thresh	(K_main,div + K_side,div)/2	(K_main,div + K_side,div)/2	0

This table describes the conditions and coefficients when the Loss coefficient model parameter is Idel'chik correlation.

Flow Scenario	ṁ_A	ṁ_B	ṁ_C	K_A	K_B	K_C
Stagnant	–	–	–	1 or last valid value	1 or last valid value	1 or last valid value
Diverging from node A — Invalid	>ṁ_thresh	<-ṁ_thresh	<-ṁ_thresh	0	1	1
Diverging from node B	<-ṁ_thresh	>ṁ_thresh	<-ṁ_thresh	K_main,div	0	K_side,div
Converging to node A — Invalid	<-ṁ_thresh	>ṁ_thresh	>ṁ_thresh	0	1	1
Converging to node B	>ṁ_thresh	<-ṁ_thresh	>ṁ_thresh	K_main,conv	0	K_side,conv
Converging to node C (branch) — Invalid	>ṁ_thresh	>ṁ_thresh	<-ṁ_thresh	1	1	0
Diverging from node C (branch) — Invalid	<-ṁ_thresh	<-ṁ_thresh	>ṁ_thresh	1	1	0

In stagnant flow, the mass flow rate conditions do not match any defined flow scenario. Stagnant flow is permitted at the start of the simulation, but the block does not revert to stagnant flow after it has achieved another mode. The mass flow rate threshold, which is the point at which the flow in the pipe begins to reverse direction, is

${\dot{m}}_{t h r e s h} = {Re}_{c} υ \bar{ρ} \sqrt{\frac{π}{4} A_{\min}},$

where:

Re_c is the Critical Reynolds number parameter, beyond which the transitional flow regime begins.
ν is the fluid viscosity.
$\bar{ρ}$ is the average fluid density.
A_min is the smallest cross-sectional area in the pipe junction.

Idel'chik Correlation Coefficient Model

When you set the Loss coefficient model parameter to Idel'chik correlation, the block calculates the pipe loss coefficients according to [2].

Flow Configuration

The block supports two flow configurations between the main branch from ports A and B and the side branch from port C. The side branch is offset from the main branch at an angle α, which is the value of the Junction angle between (A-C) parameter.

In a converging flow, the flow enters at ports A and C and exits at port B.

In a diverging flow, the flow enters at port B and exits at ports A and C.

You can control the block behavior in a prohibited flow configuration by using the Report when flow configuration is invalid parameter. If the Report when flow configuration is invalid parameter is set to None or Warning, the model continues to run in the prohibited flow configuration, but the results may not be correct.

Converging Flow

For a converging flow, the block calculates the loss coefficient of the side branch between ports C and B using a simplified version of Idel'chik that assumes the area of the main branch is constant. The loss coefficient of the side branch is

$K_{s i d e, c o n v} = [1 + {(\frac{{\dot{m}}_{C}}{{\dot{m}}_{B}} \frac{A_{B}}{A_{C}})}^{2} - 2 (\frac{A_{B}}{A_{A}}) {(1 - \frac{{\dot{m}}_{C}}{{\dot{m}}_{B}})}^{2} - 2 * \cos α * \frac{A_{B}}{A_{C}} {(\frac{{\dot{m}}_{C}}{{\dot{m}}_{B}})}^{2}] {[\frac{{\dot{m}}_{C}}{{\dot{m}}_{B}} \frac{A_{C}}{A_{B}}]}^{- 2},$

where:

${\dot{m}}_{A}, {\dot{m}}_{B}, {\dot{m}}_{C}$ are the mass flow rates from rates at ports A, B, and C, respectively.
A_A, A_B, A_C are fitting coefficients for ports A, B, and C, respectively.

The block calculates the loss coefficient of the main branch between ports A and B using a simplified version of Idel'chik that assumes the main branch area is constant and $Q_{C} = Q_{B} + Q_{S}$ , where Q is the volumetric flow rate through the specified port. The main branch loss coefficient is

$K_{m a i n, c o n v} = [1 - {(1 - \frac{{\dot{m}}_{C}}{{\dot{m}}_{B}})}^{2} - 2 * \cos α * \frac{A_{B}}{A_{C}} {(\frac{{\dot{m}}_{C}}{{\dot{m}}_{B}})}^{2}] {[1 - {(\frac{{\dot{m}}_{C}}{{\dot{m}}_{B}})}^{2}]}^{- 1} .$

Diverging Flow

For a diverging flow, the block calculates the loss coefficient of the side branch between ports C and B as

$K_{s i d e, d i v} = A' [1 + {(\frac{{\dot{m}}_{C}}{{\dot{m}}_{B}} \frac{A_{B}}{A_{C}})}^{2} - 2 * \cos α * \frac{{\dot{m}}_{C}}{{\dot{m}}_{B}} \frac{A_{B}}{A_{C}}] {[\frac{{\dot{m}}_{C}}{{\dot{m}}_{B}} \frac{A_{C}}{A_{B}}]}^{- 2},$

where

$A'= \frac{1}{2} [1 + \tanh (\frac{4 (R_{A^{'}} - 0.8)}{0.8})] + \frac{0.9}{2} [1 - \tanh (\frac{4 (R_{A^{'}} - 0.8)}{0.8})]$

and

$R_{A^{'}} = \frac{\sqrt{{\dot{m}}_{C}^{2} + {\dot{m}}_{t h r e s h}^{2}}}{\sqrt{{\dot{m}}_{B}^{2} + {\dot{m}}_{t h r e s h}^{2}}} .$

The block calculates the loss coefficient of the main branch between ports A and B as

$K_{m a i n, d i v} = 0.4 {(1 - \frac{{\dot{m}}_{A}}{{\dot{m}}_{B}} \frac{A_{B}}{A_{A}})}^{2} {(\frac{{\dot{m}}_{A}}{{\dot{m}}_{B}})}^{- 2} .$

Custom Y-Junction

When you set the Loss coefficient model parameter to Custom, the block calculates the pipe loss coefficient at each port, K, based on the user-defined loss parameters for converging and diverging flow and mass flow rate at each port. You must specify K_main,conv, K_main,div, K_side,conv, and K_side,div as the Main branch converging loss coefficient, Main branch diverging loss coefficient, Side branch converging loss coefficient, and Side branch diverging loss coefficient parameters, respectively. The custom loss coefficient model behavior for the Y-junction is the same as for the custom T-junction.

Mass and Momentum Balance

The block conserves mass in the junction such that

$\begin{array}{l} {\dot{m}}_{A} + {\dot{m}}_{B} + {\dot{m}}_{C} = 0 \\ {\dot{m}}_{w A} + {\dot{m}}_{w B} + {\dot{m}}_{w C} = 0 \\ {\dot{m}}_{g A} + {\dot{m}}_{g B} + {\dot{m}}_{g C} = 0 \\ {\dot{m}}_{d A} + {\dot{m}}_{d B} + {\dot{m}}_{d C} = 0 \end{array}$

ṁ_i is the mixture mass flow rate for a given port, i.
$\dot{m}$ _wi is the water vapor mass flow rate for a given port, i.
$\dot{m}$ _gi is the trace gas mass flow rate for a given port, i.
$\dot{m}$ _di is the water droplet mass flow rate for a given port, i.

Flow through the pipe junction behaves according to the momentum conservation equations between ports A, B, and C:

$\begin{array}{l} p_{A} - p_{I} = I_{A} + \frac{K_{A}}{2 \bar{ρ} A_{_{m a i n}}^{2}} {\dot{m}}_{A} \sqrt{{\dot{m}}_{A}^{2} + {\dot{m}}_{t h r e s h}^{2}} \\ p_{B} - p_{I} = I_{B} + \frac{K_{B}}{2 \bar{ρ} A_{_{m a i n}}^{2}} {\dot{m}}_{B} \sqrt{{\dot{m}}_{B}^{2} + {\dot{m}}_{t h r e s h}^{2}} \\ p_{C} - p_{I} = I_{C} + \frac{K_{C}}{2 \bar{ρ} A_{_{s i d e}}^{2}} {\dot{m}}_{C} \sqrt{{\dot{m}}_{C}^{2} + {\dot{m}}_{t h r e s h}^{2}} \end{array}$

where I represents the fluid inertia, and

$\begin{array}{l} I_{A} = {\ddot{m}}_{A} \frac{\sqrt{π \cdot A_{s i d e}}}{A_{m a i n}} \\ I_{B} = {\ddot{m}}_{B} \frac{\sqrt{π \cdot A_{s i d e}}}{A_{m a i n}} \\ I_{C} = {\ddot{m}}_{C} \frac{\sqrt{π \cdot A_{m a i n}}}{A_{s i d e}} \end{array}$

A_main is the Main branch area (A-B) parameter and A_side is the Side branch area (C) parameter.

Energy Balance

The block balances energy such that

$ϕ_{A} + ϕ_{B} + ϕ_{C} = 0,$

where:

ϕ_A is the energy flow rate at port A.
ϕ_B is the energy flow rate at port B.
ϕ_C is the energy flow rate at port C.

Variables

To set the priority and initial target values for the block variables prior to simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.

Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources, one of which is the Nominal Values section in the block dialog box or Property Inspector. For more information, see Modify Nominal Values for a Block Variable.

Ports

Conserving

expand all

A — Moist air port
moist air

Moist air conserving port associated with the liquid entrance or exit of the junction.

B — Moist air port
moist air

Moist air conserving port associated with the liquid entrance or exit of the junction.

C — Moist air port
moist air

Moist air conserving port associated with the liquid entrance or exit of the junction.

Parameters

expand all

Main branch area (A-B) — Cross-sectional area between ports A and B
`0.01 m^2` (default) | positive scalar

Area of connecting pipe between ports A and B.

Side branch area (C) — Cross-sectional area of the side branch
`0.004` `m^2` (default) | positive scalar

Area of connecting pipe between port C and the main branch.

Loss coefficient model — Loss coefficient type
`Idel'chik correlation` (default) | `Custom`

Junction loss coefficient model. Set this parameter to Custom to specify individual diverging and converging loss coefficients for each flow path segment.

Loss coefficient configuration change time constant — Time scale of smoothing function
`0.0001 s` (default) | positive scalar

Time scale of the smoothing function. Use this parameter to ensure smooth transitions by tuning the block dynamic behavior during flow reversals.

Laminar flow pressure ratio — Pressure ratio at which flow transitions between laminar and turbulent regimes
`0.999` (default) | positive scalar

Pressure ratio at which the moist air flow transitions between the laminar and turbulent regimes.

Zero-flow threshold pressure ratio — Pressure ratio that corresponds to stagnant flow
`0.999999` (default) | positive scalar

Pressure ratio that the block uses to calculate the threshold beneath which the flow is stagnant. The block uses this threshold to reduce numerical chatter during simulation.