Hybrid Scheme in the Genetic Algorithm
This example shows how to use a hybrid scheme to optimize a function using the genetic algorithm and another optimization method. ga can quickly reach a neighborhood of a local minimum, but it can require many function evaluations to achieve convergence. To speed the solution process, first run ga for a small number of generations to approach an optimum point. Then use the solution from ga as the initial point for another optimization solver to perform a faster and more efficient local search.
Rosenbrock's Function
This example uses Rosenbrock's function (also known as Dejong's second function) as the fitness function:
.
Rosenbrock's function is notorious in optimization because of the slow convergence most methods exhibit when trying to minimize this function. Rosenbrock's function has a unique minimum at the point x* = (1,1), where it has a function value .
The code for Rosenbrock's function is in the dejong2fcn file.
type dejong2fcn.mfunction scores = dejong2fcn(pop)
%DEJONG2FCN Compute DeJongs second function.
%This function is also known as Rosenbrock's function
% Copyright 2003-2004 The MathWorks, Inc.
scores = zeros(size(pop,1),1);
for i = 1:size(pop,1)
p = pop(i,:);
scores(i) = 100 * (p(1)^2 - p(2)) ^2 + (1 - p(1))^2;
end
Plot Rosenbrock's function over the range –2 <= x(1) <= 2; –2 <= x(2) <=2.
plotobjective(@dejong2fcn,[-2 2;-2 2]);

Genetic Algorithm Solution
First, use ga alone to find the minimum of Rosenbrock's function.
FitnessFcn = @dejong2fcn; numberOfVariables = 2;
Include plot functions to monitor the optimization process.
options = optimoptions(@ga,'PlotFcn',{@gaplotbestf,@gaplotstopping});Set the random number stream for reproducibility, and run ga using the options.
rng default
[x,fval] = ga(FitnessFcn,numberOfVariables,[],[],[],[],[],[],[],options)ga stopped because the average change in the fitness value is less than options.FunctionTolerance.

x = 1×2
0.3454 0.1444
fval = 0.4913
Using the default stopping criteria, ga does not provide a very accurate solution. You can change the stopping criteria to try to find a more accurate solution, but ga requires many function evaluations to approach the global optimum x* = (1,1).
Instead, perform a more efficient local search that starts where ga stops by using the hybrid function option in ga.
Adding a Hybrid Function
A hybrid function begins from the point where ga stops. Hybrid function choices are fminsearch, patternsearch, or fminunc. Because this optimization example is smooth and unconstrained, use fminunc as the hybrid function. Provide fminunc with plot options as an additional argument when specifying the hybrid function.
fminuncOptions = optimoptions(@fminunc,'PlotFcn',{'optimplotfval','optimplotx'}); options = optimoptions(options,'HybridFcn',{@fminunc, fminuncOptions});
Run ga again with fminunc as the hybrid function.
[x,fval,exitflag,output] = ga(FitnessFcn,numberOfVariables,[],[],[],[],[],[],[],options)
ga stopped because the average change in the fitness value is less than options.FunctionTolerance.
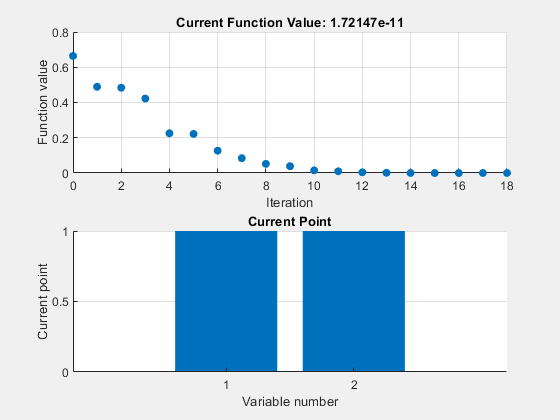
Local minimum found. Optimization completed because the size of the gradient is less than the value of the optimality tolerance. <stopping criteria details>

x = 1×2
1.0000 1.0000
fval = 1.7215e-11
exitflag = 1
output = struct with fields:
problemtype: 'unconstrained'
rngstate: [1×1 struct]
generations: 51
funccount: 2534
message: 'ga stopped because the average change in the fitness value is less than options.FunctionTolerance.↵FMINUNC: Local minimum found.↵↵Optimization completed because the size of the gradient is less than↵the value of the optimality tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The first-order optimality measure, 2.473362e-07, is less ↵than options.OptimalityTolerance = 1.000000e-06.↵'
maxconstraint: []
hybridflag: 1
The ga plot shows the best and mean values of the population in every generation. The plot title identifies the best value found by ga when it stops. The hybrid function fminunc starts from the best point found by ga. The fminunc plot shows the solution x and fval, which result from using ga and fminunc together. In this case, using a hybrid function improves the accuracy and efficiency of the solution. The output.hybridflag field shows that fminunc stops with exit flag 1, indicating that x is a true local minimum.