Optimize Data Types for an FPGA with DSP Slices
This example shows how to use the addSpecification method of the fxpOptimizationOptions class to achieve better mapping for product blocks on DSP slices for FPGA targets. Use addSpecification to specify known data types in a system. After specifying these known parameters, when you optimize data types in the system, the optimization process does not change the specified block parameter data type.
Many FPGA boards have specific multiply-accumulate hardware accelerators, called DSP slices that speed up the execution of signal processing functions. DSP slices vary in size depending on the vendor. To gain the hardware acceleration benefits of DSP slices, it is common in FPGA design to map multiply and accumulate operations in the algorithm onto these slices.
In this example, optimize data types for 3 DSP families of Xilinx® boards, as well as for a generic 18x18 bit input. Use the addSpecification method to achieve a good mapping between the Product blocks in the design and the target DSP slices.
This example makes the following assumptions:
Only Product and Gain blocks are targeted for mapping to DSP slices. You can handle other blocks in a similar fashion.
Product blocks have only 2 inputs.
Driver blocks (blocks that precede Product or Gain blocks) have
OutDataTypeStras a parameter.Only blocks that do not have the HDL property DSPStyle set to
offare targeted.
Instrument the Model and Collect Ranges
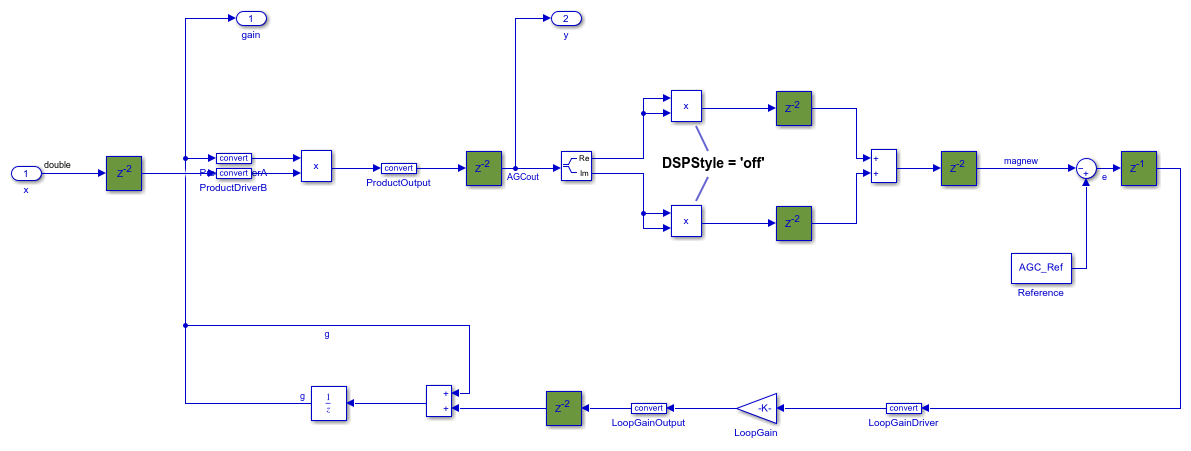
To begin, open the system for which you want to optimize data types. In this example, data types are optimized for an automatic gain control algorithm.
model = 'mQAMAGC'; sud = [model '/Automatic Gain Control']; open_system(model);
Initialize the QAM Tx subsystem.
initQAM;
Create a structure array that describes the properties of the target DSP slice. The dspStyle function included in this example provides information about common Xilinx® DSP slices including DSP48A1 (18x18 bit signed), DSP48E1 (18x25 bit signed), and DSP48E2 (18x27 bit signed). It also provides an example of a generic 18x18 signed DSP slice.
dspStyle = getDSPStyle('DSP48E2');
In this example, only Product and Gain blocks are targeted for mapping to DSP slices. Find all the Product and Gain blocks in the system under design that do not have the HDL block property DSPStyle set to off. For more information, see DSPStyle (HDL Coder).
productBlocks = find_system(sud,'LookUnderMasks','on','BlockType','Product'); hasDSPOff = cellfun(@(x)(isequal(hdlget_param(x,'DSPStyle'),'off')), productBlocks); productDSP = productBlocks(~hasDSPOff); gainBlocks = find_system(sud,'LookUnderMasks','on','BlockType','Gain'); hasDSPOff = cellfun(@(x)(isequal(hdlget_param(x,'DSPStyle'),'off')), productBlocks); gainDSP = gainBlocks(~hasDSPOff);
Enable instrumentation to log minimum, maximum, and overflow data during simulation for Product blocks and driver blocks that precede Product blocks. Simulate the model to collect ranges.
c = DataTypeWorkflow.Converter(sud,'TopModel',model); c.CurrentRunName = 'RangeCollection'; c.simulateSystem('MinMaxOverflowLogging','MinMaxAndOverflow');
Get Specifications for Product Blocks
For efficient mapping of Product blocks to available DSP slices, consider the range requirements of the Product blocks. Create a structure array to store simulation minimum and maximum values for Product blocks collected during the range collection run.
specs = struct('Block',productDSP{1},'Drivers',[],'Min',[],'Max',[]); %#ok<*SAGROW> r = c.results(c.CurrentRunName,@(x)(strcmp(x.ResultName,productDSP{1}))); specs.Min = r.SimMin; specs.Max = r.SimMax; predecessorBlocks = predecessors(productDSP{1}); for pIndex = 1:numel(predecessorBlocks) pBlkObj = get_param(predecessorBlocks{pIndex},'Object'); specs.Drivers(pIndex) = pBlkObj.Handle; r = c.results(c.CurrentRunName,@(x)(strcmp(x.ResultName,pBlkObj.getFullName()))); specs.Min(pIndex+1) = r.SimMin; specs.Max(pIndex+1) = r.SimMax; end
Store these known parameter specifications for the Product blocks in a Simulink.Simulation.BlockParameter object.
bpProductBlock = Simulink.Simulation.BlockParameter.empty(0,3); fout = fi(max([abs(specs.Min(1)) abs(specs.Max(1))]),dspStyle.sout,dspStyle.wout); bpProductBlock(1) = Simulink.Simulation.BlockParameter(specs.Block, ... 'OutDataTypeStr', ... sprintf('fixdt(%i,%i,%i)',dspStyle.sout,dspStyle.wout,fout.FractionLength));
Assign the largest type to the largest range of the driver blocks. This ensures that the largest data type available in the target hardware is applied to the block with the largest range requirement.
dMax1 = max([abs(specs.Min(2)) abs(specs.Max(2))]); dMax2 = max([abs(specs.Min(3)) abs(specs.Max(3))]); if dMax1 < dMax2 win_1 = dspStyle.win_1; sin_1 = dspStyle.sin_1; win_2 = dspStyle.win_2; sin_2 = dspStyle.sin_2; if dspStyle.win_1 >= dspStyle.win_2 win_1 = dspStyle.win_2; sin_1 = dspStyle.sin_2; win_2 = dspStyle.win_1; sin_2 = dspStyle.sin_1; end else win_1 = dspStyle.win_2; sin_1 = dspStyle.sin_2; win_2 = dspStyle.win_1; sin_2 = dspStyle.sin_1; if dspStyle.win_1 >= dspStyle.win_2 win_1 = dspStyle.win_1; sin_1 = dspStyle.sin_1; win_2 = dspStyle.win_2; sin_2 = dspStyle.sin_2; end end
Get specifications for blocks preceding Product blocks. Note that this example assumes that Product blocks have two inputs.
fin1 = fi(dMax1, sin_1, win_1); blkObj = get_param(specs.Drivers(1), 'Object'); bpProductBlock(2) = Simulink.Simulation.BlockParameter(blkObj.getFullName, ... 'OutDataTypeStr', ... sprintf('fixdt(%i, %i, %i)', sin_1, win_1, fin1.FractionLength)); fin2 = fi(dMax2, sin_2, win_2); blkObj = get_param(specs.Drivers(2), 'Object'); bpProductBlock(3) = Simulink.Simulation.BlockParameter(blkObj.getFullName, ... 'OutDataTypeStr', ... sprintf('fixdt(%i, %i, %i)', sin_2, win_2, fin2.FractionLength));
Get Specifications for Gain Blocks
Store known parameter specifications for the Gain blocks in a Simulink.Simulation.BlockParameter object.
bpGainBlock = Simulink.Simulation.BlockParameter.empty(0,3); specs = struct('Block',gainDSP{1},'Drivers',[],'Min',[],'Max',[]); %#ok<*SAGROW> r = c.results(c.CurrentRunName,@(x)(strcmp(x.ResultName,gainDSP{1}))); specs.Min = r.SimMin; specs.Max = r.SimMax; predecessorBlocks = predecessors(gainDSP{1}); pBlkObj = get_param(predecessorBlocks{1},'Object'); specs.Drivers(1) = pBlkObj.Handle; r = c.results(c.CurrentRunName,@(x)(strcmp(x.ResultName,pBlkObj.getFullName()))); specs.Min(2) = r.SimMin; specs.Max(2) = r.SimMax;
Get specifications for the output of Gain blocks.
fout = fi(max(abs([specs.Min(1) specs.Max(1)])),dspStyle.sout,dspStyle.wout);
bpGainBlock(1) = Simulink.Simulation.BlockParameter(gainDSP{1}, ...
'OutDataTypeStr', ...
sprintf('fixdt(%i, %i, %i)',dspStyle.sout,dspStyle.wout,fout.FractionLength));
Get specifications for the blocks preceding Gains blocks and assign this to the first configuration of the Simulink.Simulation.BlockParameter object bpGainBlock.
blkObj = get_param(specs.Drivers(1),'Object'); fin = fi(max(abs([specs.Min(2) specs.Max(2)])),dspStyle.sin_1,dspStyle.win_1); bpGainBlock(2) = Simulink.Simulation.BlockParameter(blkObj.getFullName, ... 'OutDataTypeStr', ... sprintf('fixdt(%i,%i,%i)',dspStyle.sin_1,dspStyle.win_1,fin.FractionLength));
Get specifications for the Gain parameter of the system under design and assign this value to the second configuration of bpGainBlock.
paramValue = str2double(get_param(sud,'AGC_Gain')); fParam = fi(paramValue,dspStyle.sin_2,dspStyle.win_2); bpGainBlock(3) = Simulink.Simulation.BlockParameter(gainDSP{1}, ... 'ParamDataTypeStr', ... sprintf('fixdt(%i,%i,%i)',dspStyle.sin_2,dspStyle.win_2,fParam.FractionLength));
Define Constraints and Tolerances
Create an fxpOptimizationOptions object to define constraints and tolerances. Specify allowed word lengths of 8 bits to 32 bits.
options = fxpOptimizationOptions('AllowableWordLengths',8:2:32);
Use the addTolerance method to define tolerances for the differences between the original behavior of the system and the behavior using the optimized fixed-point data types.
addTolerance(options,sud,1,'RelTol',1e-2); addTolerance(options,sud,2,'RelTol',1e-2); addTolerance(options,sud,1,'AbsTol',1e-3); addTolerance(options,sud,2,'AbsTol',1e-3);
Use the addSpecification method to define specifications for the Product and Gain blocks.
addSpecification(options,'BlockParameter',bpProductBlock); % set the specifications for the product block addSpecification(options,'BlockParameter',bpGainBlock); % set the specifications for the gain block showSpecifications(options);
Index Name BlockPath Value
_____ ________________ _____________________________________________ __________________
1 OutDataTypeStr mQAMAGC/Automatic Gain Control/LoopGain 'fixdt(1, 45, 53)'
2 ParamDataTypeStr mQAMAGC/Automatic Gain Control/LoopGain 'fixdt(1,27,35)'
3 OutDataTypeStr mQAMAGC/Automatic Gain Control/LoopGainDriver 'fixdt(1,18,16)'
4 OutDataTypeStr mQAMAGC/Automatic Gain Control/Product 'fixdt(1,45,43)'
5 OutDataTypeStr mQAMAGC/Automatic Gain Control/ProductDriverA 'fixdt(1, 27, 25)'
6 OutDataTypeStr mQAMAGC/Automatic Gain Control/ProductDriverB 'fixdt(1, 18, 17)'
varSpecs
________
Optimize Fixed-Point Data Types
Use the fxpopt function to run the optimization. The software analyzes ranges of objects in the system under design and the constraints specified in the fxpOptimizationOptions object to apply heterogeneous data types to your system while minimizing the total bit width. Known parameter specifications included using the addSpecification method is not affected by the optimization process.
result = fxpopt(model,sud,options);
+ Starting data type optimization... + Checking for unsupported constructs. + Preprocessing + Modeling the optimization problem - Constructing decision variables + Running the optimization solver Backing up simulation data to base workspace. To skip this operation, set Export=false. - Evaluating new solution: cost 200, does not meet the behavioral constraints. - Evaluating new solution: cost 250, does not meet the behavioral constraints. - Evaluating new solution: cost 300, does not meet the behavioral constraints. - Evaluating new solution: cost 350, does not meet the behavioral constraints. - Evaluating new solution: cost 400, does not meet the behavioral constraints. - Evaluating new solution: cost 450, does not meet the behavioral constraints. - Evaluating new solution: cost 500, meets the behavioral constraints. - Updated best found solution, cost: 500 - Evaluating new solution: cost 496, meets the behavioral constraints. - Updated best found solution, cost: 496 - Evaluating new solution: cost 492, meets the behavioral constraints. - Updated best found solution, cost: 492 - Evaluating new solution: cost 488, meets the behavioral constraints. - Updated best found solution, cost: 488 - Evaluating new solution: cost 484, meets the behavioral constraints. - Updated best found solution, cost: 484 - Evaluating new solution: cost 480, meets the behavioral constraints. - Updated best found solution, cost: 480 - Evaluating new solution: cost 478, meets the behavioral constraints. - Updated best found solution, cost: 478 - Evaluating new solution: cost 476, does not meet the behavioral constraints. - Evaluating new solution: cost 472, does not meet the behavioral constraints. - Evaluating new solution: cost 476, meets the behavioral constraints. - Updated best found solution, cost: 476 - Evaluating new solution: cost 474, meets the behavioral constraints. - Updated best found solution, cost: 474 - Evaluating new solution: cost 468, meets the behavioral constraints. - Updated best found solution, cost: 468 - Evaluating new solution: cost 458, meets the behavioral constraints. - Updated best found solution, cost: 458 - Evaluating new solution: cost 454, meets the behavioral constraints. - Updated best found solution, cost: 454 - Evaluating new solution: cost 450, meets the behavioral constraints. - Updated best found solution, cost: 450 - Evaluating new solution: cost 446, meets the behavioral constraints. - Updated best found solution, cost: 446 - Evaluating new solution: cost 442, meets the behavioral constraints. - Updated best found solution, cost: 442 - Evaluating new solution: cost 438, meets the behavioral constraints. - Updated best found solution, cost: 438 - Evaluating new solution: cost 436, meets the behavioral constraints. - Updated best found solution, cost: 436 - Evaluating new solution: cost 434, does not meet the behavioral constraints. - Evaluating new solution: cost 430, does not meet the behavioral constraints. - Evaluating new solution: cost 434, meets the behavioral constraints. - Updated best found solution, cost: 434 - Evaluating new solution: cost 432, meets the behavioral constraints. - Updated best found solution, cost: 432 - Evaluating new solution: cost 426, meets the behavioral constraints. - Updated best found solution, cost: 426 - Evaluating new solution: cost 416, meets the behavioral constraints. - Updated best found solution, cost: 416 - Evaluating new solution: cost 412, meets the behavioral constraints. - Updated best found solution, cost: 412 - Evaluating new solution: cost 408, meets the behavioral constraints. - Updated best found solution, cost: 408 - Evaluating new solution: cost 404, meets the behavioral constraints. - Updated best found solution, cost: 404 - Evaluating new solution: cost 400, meets the behavioral constraints. - Updated best found solution, cost: 400 - Evaluating new solution: cost 396, meets the behavioral constraints. - Updated best found solution, cost: 396 - Evaluating new solution: cost 394, meets the behavioral constraints. - Updated best found solution, cost: 394 - Evaluating new solution: cost 392, does not meet the behavioral constraints. - Evaluating new solution: cost 388, does not meet the behavioral constraints. - Evaluating new solution: cost 392, meets the behavioral constraints. - Updated best found solution, cost: 392 - Evaluating new solution: cost 390, meets the behavioral constraints. - Updated best found solution, cost: 390 - Evaluating new solution: cost 384, meets the behavioral constraints. - Updated best found solution, cost: 384 - Evaluating new solution: cost 374, meets the behavioral constraints. - Updated best found solution, cost: 374 - Evaluating new solution: cost 370, meets the behavioral constraints. - Updated best found solution, cost: 370 - Evaluating new solution: cost 366, meets the behavioral constraints. - Updated best found solution, cost: 366 - Evaluating new solution: cost 362, meets the behavioral constraints. - Updated best found solution, cost: 362 - Evaluating new solution: cost 358, meets the behavioral constraints. - Updated best found solution, cost: 358 - Evaluating new solution: cost 354, meets the behavioral constraints. - Updated best found solution, cost: 354 - Evaluating new solution: cost 352, meets the behavioral constraints. - Updated best found solution, cost: 352 - Evaluating new solution: cost 350, does not meet the behavioral constraints. - Evaluating new solution: cost 346, does not meet the behavioral constraints. - Evaluating new solution: cost 350, meets the behavioral constraints. - Updated best found solution, cost: 350 - Evaluating new solution: cost 348, meets the behavioral constraints. - Updated best found solution, cost: 348 - Evaluating new solution: cost 342, does not meet the behavioral constraints. - Evaluating new solution: cost 338, does not meet the behavioral constraints. - Evaluating new solution: cost 344, does not meet the behavioral constraints. + Optimization has finished. - Neighborhood search complete. - Maximum number of iterations completed. + Fixed-point implementation that satisfies the behavioral constraints found. The best found solution is applied on the model. - Total cost: 348 - Maximum absolute difference: 0.006126 - Use the explore method of the result to explore the implementation.
Use the explore method of the OptimizationResult object, result, to open the Simulation Data Inspector and explore the design.
explore(result)
ans =
OptimizationSolution with properties:
Cost: 348
Pass: 1
MaxDifference: 0.0061
RunID: 24040
RunName: {'solution_56ed4ad01b357d644b124a742c8b97a4bc862de7_1'}
