How to Set CORDIC Input Word Length and Maximum Shift Value to Achieve Desired Precision

This example shows that when using CORDIC-based algorithms in MATLAB® and Simulink®, to achieve a precision equivalent to L bits, you can set the input fraction length to L+log2(L+integerLength) and the CORDIC maximum shift value to L+integerLength as a starting point. In cases where the computation error is difficult to estimate analytically, you can then use numeric simulation to further refine the CORDIC configuration necessary to achieve the required accuracy.

CORDIC (COordinate Rotation DIgital Computer) is a hardware efficient algorithm that only requires iterative shift-add operations [1]. The CORDIC algorithm eliminates the need for explicit multipliers and is suitable for calculating a variety of functions, including trigonometric functions, square root, divide, and logarithmic functions.

The precision of the CORDIC algorithm is a function of the data type used and the maximum shift value or number of iterations of the CORDIC kernel. Using a data type with a larger word length and performing more iterations of the CORDIC algorithm can reduce the numeric error of the result. However, doing so also increases the latency of the computation and that utilizes more hardware resources.

Use Fraction Length of L+log2(L+integerLength) and Maximum Shift Value L+integerLength to Achieve Precision 2^-L

The roundoff error of the CORDIC algorithm is approximately log2(n), where n is the number of iterations of the CORDIC kernel, as estimated by Walther [1]. More recent studies have presented further refinements on this value [2,3,4]. You can compensate for this error by selecting a data type with an extra log2(n) bits. Therefore, when using the Fixed-Point Designer™ library of CORDIC-based Simulink blocks and MATLAB functions, you can estimate that an input data type with fraction length L+log2(L+integerLength) results in an approximate precision of 2^-L. You can estimate the intergerLength based on the range of the input and intemediate data.

For most of the CORDIC-based blocks and functions, the CORDIC maximum shift value or number of iterations is automatically set by the software based on the word length of the input. When the CORDIC maximum shift value is a user settable parameter, you can set the maximum shift value to L+integerLength as a starting point to achieve a precision of approximately 2^-L.

Simulation of CORDIC Reciprocal Kernel in Linear Vectoring Mode

This example shows a reciprocal kernel calculated using the CORDIC algorithm in a linear vectoring mode using a fixed-point data type.

Define the target precision L in bits. The corresponding computation error is 2^-L.

L = 14;

The reciprocal kernel convergence range is [1,2), such that the result is within (0.5,1]. For simplicity, set both input and output to have same datatype with 1 sign bit and 1 integer bit such that it can hold values between 0.5 and 2.

signBit = 1;
inputIntegerLength = 1;

To achieve a precision of 2^-L, define an input data type with a fraction length of L+log2(L+integerLength).

inputFracLength = L+round(log2(L+inputIntegerLength));
inputWordLength = signBit+inputIntegerLength+inputFracLength;

Set the CORDIC maximum shift value equal to the desired precision of L bits plus the integer length.

maximumShiftVal = L+inputIntegerLength;

For the linear vectoring mode, the CORDIC shift sequence is 2^-1, 2^-2, ... 2^-maximumShiftVal, such that the number of iterations is equal to the CORDIC maximum shift value, maximumShiftVal. Note that the CORDIC shift sequence varies slightly based on the CORDIC mode used, but in all cases the number of CORDIC iterations is approximately equal to the CORDIC maximum shift value [1].

shiftSeq = 1:maximumShiftVal;

Generate a test input that covers the full convergence range of the CORDIC algorithm.

x = linspace(1,2,1001);
y = ones(1,numel(x));
z = zeros(1,numel(x));

Convert the input data to a fixed-point data type with the word length and fraction length defined at the start of this example.

xfi = fi(x,signBit,inputWordLength,inputFracLength);
yfi = fi(y,signBit,inputWordLength,inputFracLength);
results = fi(z,signBit,inputWordLength,inputFracLength);

Compute the CORDIC-based reciprocal.

for i = 1:numel(x)
    for idx = shiftSeq
        [yfi(i),results(i)] = fixed.cordic.linear.vectoring.kernel(xfi(i),yfi(i),results(i),idx);
    end
end

Compute the absolute computation error, using the floating-point solution as the baseline for comparison.

Verify that the simulated error is close to the target precision for the computation. You can offset the inputFracLength away from L+log2(L+inputIntegerLength) to see the impact of the input word length on the resulting computation error.

errorInBits = log2(abs(double(results)-(1./x)));
figure;
histogram(errorInBits)
xlabel('log2(Absolute computation error)');
grid on;

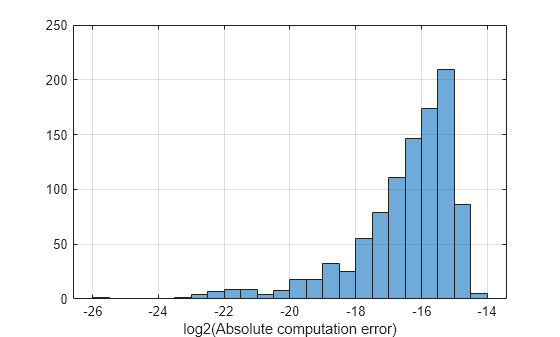
This figure shows a histogram of the computation error on a log2 scale. The computation errors are below 2^-14 and the median computation error is 2^-16. This aligns with the desired precision of 2^-14 defined at the start of this example.

cordicLinVecError = median(errorInBits(isfinite(errorInBits)))

cordicLinVecError = 
-16.0705

Simulation of CORDIC in Other Modes

CORDIC has multiple modes that can perform different computations [1]. For example, the linear vectoring mode used in the first example can compute reciprocal, circular rotation mode can compute sine and cosine functions, and hyperbolic vectoring mode can compute square root. The different CORDIC modes are all based on a similar iterative shift-add concept, but the underlying math varies slightly.

This plot shows the simulated error for different CORDIC modes with fraction length of L+log2(L+integerLength) and maximum shift value L+integerLength. Similar to the above example, these simulations include only the CORDIC kernels with minimum pre-processing or post-processing steps. These simulations cover the full convergence range. See the helper function SimulationOfMultipleCORDICKernels.mlx for more details on the generation of this plot.

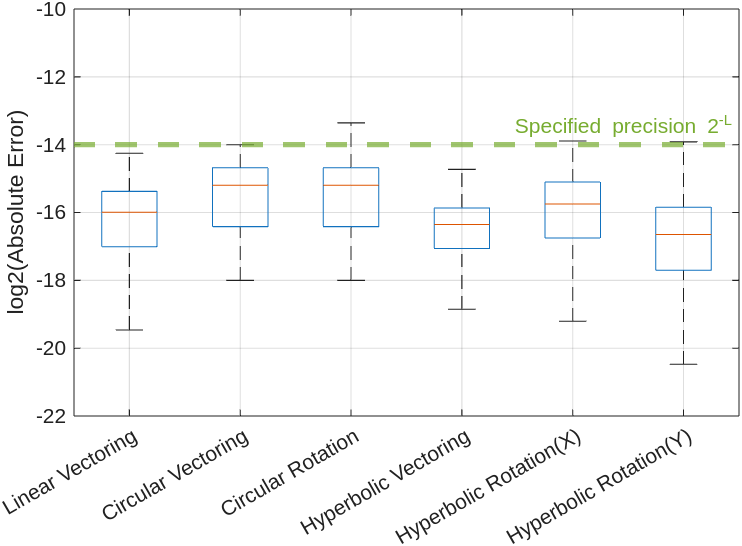
For all the CORDIC modes, with fraction length of L+log2(L+integerLength) and maximum shift value L+integerLength, the absolute error is less than or equal to 2^-L. This indicates that this configuration, where you specify a fraction length of L+log2(L+integerLength)and maximum shift value L+integerLength, can be shared across other CORDIC modes with comparable results.

Example of Real-World cordicsincos Function

The simulations in the above examples were constructed using only the CORDIC kernels with minimum supporting computations. Real-world applications typically require preprocessing and postprocessing to ensure the computation is within the CORDIC convergence range and to compensate for the CORDIC gain. In addition, some CORDIC computations require a quantized lookup table. All of these additional operations can contribute to the overall computation error and can be difficult to estimate analytically [2,3,4].

This example uses the cordicsincos function to show that an input fraction length of L+log2(L+inputIntegerLength) and maximum shift value L+inputIntegerLength is still a good starting point for CORDIC-based functions in MATLAB and Simulink, even with the additional preprocessing and postprocessing computations are included. In Simulink, you can use the Trigonometric Function block to perform trigonometric operations using the CORDIC approximation method.

Floating-Point Baseline

Construct a floating-point input within the range [-2*pi,2*pi]. Compute the floating-point solution of sine and cosine to provide a baseline for comparison with the fixed-point CORDIC-based solution.

Because the input range is [2*pi,2*pi], set the fixed point type to avoid overflow

floatInput = linspace(2,-2,81)*pi;
sin_float = sin(floatInput)';
cos_float = cos(floatInput)';

Set the initial CORDIC maximum shift value and fraction length to the recommended starting values of L+integerLength and L+log2(L+integerLength), respectively.

inputIntegerLength = 3;
signBit = 1;
inputFracLength0 = L+round(log2(L+inputIntegerLength));
wordLength0 = signBit+inputIntegerLength+inputFracLength0;
maximumShiftValue0 = L+inputIntegerLength;

CORDIC Simulation 1: Constant Maximum Shift Value With Different Fraction Lengths

The cordicsincos() function uses CORDIC in circular rotation mode. The shift sequence for the circular rotation mode is 2^0, 2^-1,...,2^-maximumShiftValue, such that the number of iterations is equal to maximumShiftValue + 1.

nIteration = maximumShiftValue0 + 1;

Try different fraction lengths around the starting point of L+log2(L+inputIntegerLength).

fracLengthOffset = -4:6;
fracLength = inputFracLength0 + fracLengthOffset;

Initialize matrices for the fixed-point results.

sin_fixed = zeros(numel(floatInput),numel(fracLength));
cos_fixed = zeros(numel(floatInput),numel(fracLength));

Compute sine and cosine using the fixed-point cordicsincos function for different word lengths around the starting value of wordLength0. Use the fiaccel function to accelerate the fixed-point simulations.

for i = 1:numel(fracLength)
    wordLength = fracLength(i) + inputIntegerLength + signBit;
    % Construct fixed-point input
    fixedInput = removefimath(fi(floatInput,1,wordLength,fracLength(i),'RoundingMethod','zero'));
    [sin_tmp, cos_tmp] = cordicsincos(fixedInput, nIteration);
    sin_fixed(:,i) = double(sin_tmp); 
    cos_fixed(:,i) = double(cos_tmp); 
end

Compute the absolute computation error, using the floating-point solution as the baseline for comparison.

plotErrorVsFractionlength(sin_fixed,sin_float,cos_fixed,cos_float,inputFracLength0,fracLength);

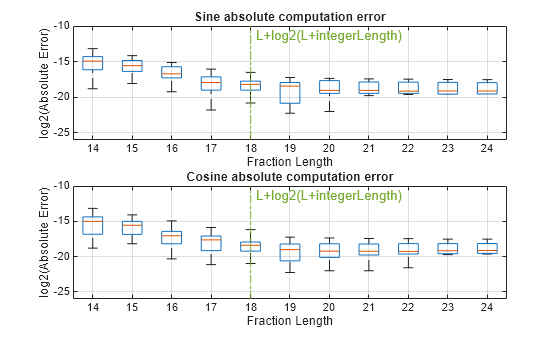
This figure shows that the absolute computation error starts to saturate when the fraction length is greater than 18 or 19 bits. This agrees with the error estimation using a datatype with 14+round(log2(14+3))=18 bits. With a fixed maximum shift value L+integerLength, further increasing the fraction length beyond L+log(L+integerLength) shows limited improvement. Because the absolute error is determined by quantization errors from various sources that can be challenging to compute analytically, numerical simulations such as those shown in this example can be used to fine-tune the optimal maximum shift value and word length [2,3,4].

CORDIC Simulation 2: Constant Data Type With Different Maximum Shift Values

This example repeats the computation of the cordicsincos function using one fixed-point data type while varying the maximum shift value (or number of iterations) of the CORDIC algorithm.

fixedInput = removefimath(fi(floatInput,1,wordLength0,inputFracLength0,'RoundingMethod','zero'));
maximumShiftValOffsets = -7:3;
maximumShiftVals = maximumShiftValue0+maximumShiftValOffsets;
nIterations = maximumShiftVals+1;
sin_fixed = zeros(numel(fixedInput),numel(maximumShiftVals),'like',fixedInput);
cos_fixed = zeros(numel(fixedInput),numel(maximumShiftVals),'like',fixedInput);

Compute sine and cosine using the fixed-point cordicsincos function for different maximum shift values. Use the fiaccel function to accelerate the fixed-point simulations.

for i = 1:numel(maximumShiftVals)
    [sin_fixed(:,i), cos_fixed(:,i)] = cordicsincos(fixedInput, nIterations(i));
end

Compute the absolute computation error, using the floating-point solution as the baseline for comparison.

plotErrorVsMaxShiftVal(sin_fixed,sin_float,cos_fixed,cos_float,maximumShiftValue0,maximumShiftVals);

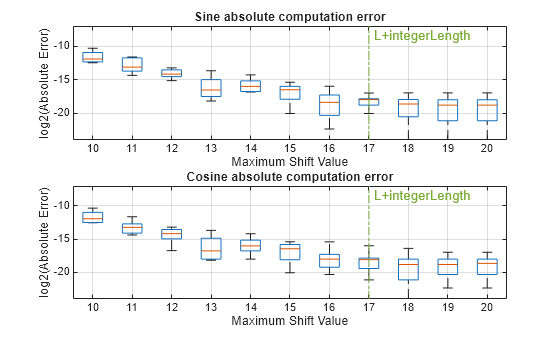
This figure shows that the absolute computation error starts to saturate when the CORDIC maximum shift value is greater than 18 and roughly agrees with the estimated value of 17. With a fixed word length of L+integerLength+log2(L+integerLength), further increasing the maximum shift value or number of iterations beyond L+integerLength shows limited improvement.

References

[1] J.S. Walther, “A Unified Algorithm for Elementary Functions,” AFIPS '71 (Spring): Proceedings of the May 18-20, 1971, Spring Joint Computer Conference, (Spring 1971): 379-385.

[2] Yu Hen Hu, "The Quantization Effects of the CORDIC Algorithm," IEEE Transactions on Signal Processing, 40, no. 4 (April 1992): 834-844.

[3] Kishore Kota and Joseph R. Cavallaro, "Numerical Accuracy and Hardware Tradeoffs for CORDIC Arithmetic for Special-Purpose Processors," IEEE Transactions on Computers, 42 no. 7 (July 1993): 769-779.

[4] Tze-Yun Sung and Hsi-Chin Hsin, "Fixed-Point Error Analysis of CORDIC Arithmetic for Special-Purpose Signal Processors," IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, E90-A no. 9 (September 2007): 2006-2013.