optSensByMertonFFT

Option price and sensitivities by Merton76 model using FFT and FRFT

Syntax

[PriceSens,StrikeOut] = optSensByMertonFFT(Rate,AssetPrice,Settle,Maturity,OptSpec,Strike,Sigma,MeanJ,JumpVol,JumpFreq)

[PriceSens,StrikeOut] = optSensByMertonFFT(___,Name,Value)

Description

[PriceSens,StrikeOut] = optSensByMertonFFT(Rate,AssetPrice,Settle,Maturity,OptSpec,Strike,Sigma,MeanJ,JumpVol,JumpFreq) computes vanilla European option price and sensitivities by Merton76 model, using Carr-Madan FFT and Chourdakis FRFT methods.

Note

Alternatively, you can use the Vanilla object to calculate price or sensitivities for vanilla options. For more information, see Get Started with Workflows Using Object-Based Framework for Pricing Financial Instruments.

[PriceSens,StrikeOut] = optSensByMertonFFT(___,Name,Value) adds optional name-value pair arguments.

Examples

Workflow for Plotting an Option Sensitivity Surface Using the Merton76 Model

Use optSensByMertonFFT to calibrate the FFT strike grid for sensitivities, compute option sensitivities, and plot option sensitivity surfaces.

Define Option Variables and Merton76 Model Parameters

AssetPrice = 80;
Rate = 0.03;
DividendYield = 0.02;
OptSpec = 'call';

Sigma = 0.16;
MeanJ = 0.02;
JumpVol = 0.08;
JumpFreq = 2;

Compute the Option Prices for the Entire FFT (or FRFT) Strike Grid, Without Specifying "Strike"

Compute option sensitivities and also output the corresponding strikes. If the Strike input is empty ( [] ), option sensitivities will be computed on the entire FFT (or FRFT) strike grid. The FFT (or FRFT) strike grid is determined as exp(log-strike grid), where each column of the log-strike grid has NumFFT points with LogStrikeStep spacing that are roughly centered around each element of log(AssetPrice). The default value for NumFFT is 2^12. In addition to the sensitivities in the first output, the optional last output contains the corresponding strikes.

Settle = datetime(2017,6,29);
Maturity = datemnth(Settle, 6);
Strike = []; % Strike is not specified

[Delta, Kout] = optSensByMertonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ...
    Sigma, MeanJ, JumpVol, JumpFreq, 'DividendYield', DividendYield, 'OutSpec', "delta");

% Show the lowest and highest strike values on the FFT strike grid
format
[Kout(1) Kout(end)]

ans = 1×2
10138 ×

    0.0000    1.8798

% Show a subset of the strikes and corresponding option sensitivities
Range = (2046:2052);
[Kout(Range) Delta(Range)]

ans = 7×2

   50.4929    0.9895
   58.8640    0.9801
   68.6231    0.8816
   80.0000    0.5283
   93.2631    0.1551
  108.7251    0.0241
  126.7505    0.0025

Change the Number of FFT (or FRFT) Points and Compare with optSensByMertonNI

Try a different number of FFT (or FRFT) points, and compare the results with numerical integration. Unlike optSensByMertonFFT, which uses FFT (or FRFT) techniques for fast computation across the whole range of strikes, the optSensByMertonNI function uses direct numerical integration and it is typically slower, especially for multiple strikes. However, the values computed by optSensByMertonNI can serve as a benchmark for adjusting the settings for optSensByMertonFFT.

% Try a smaller number of FFT points 
% (e.g. for faster performance or smaller memory footprint)
NumFFT = 2^10; % Smaller than the default value of 2^12
Strike = []; % Strike is not specified (will use the entire FFT strike grid)
[Delta, Kout] = optSensByMertonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ...
    Sigma, MeanJ, JumpVol, JumpFreq, 'DividendYield', DividendYield, 'OutSpec', "delta", ...
    'NumFFT', NumFFT);

% Compare with numerical integration method
Range = (510:516);
Strike = Kout(Range);
DeltaFFT = Delta(Range);
DeltaNI = optSensByMertonNI(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ...
    Sigma, MeanJ, JumpVol, JumpFreq, 'DividendYield', DividendYield, 'OutSpec', "delta");
Error = abs(DeltaFFT-DeltaNI);
table(Strike, DeltaFFT, DeltaNI, Error)

ans=7×4 table
    Strike     DeltaFFT      DeltaNI        Error   
    ______    __________    __________    __________

    12.696       0.89726       0.99002      0.092766
    23.449       0.93421       0.99002       0.05581
    43.312       0.94691       0.99001      0.043093
        80       0.50983       0.52827      0.018446
    147.76      0.004147    0.00019101      0.003956
    272.93      0.001071     1.547e-09      0.001071
    504.11    0.00030521    5.7578e-10    0.00030521

Make Further Adjustments to FFT (or FRFT)

If the values in the output DeltaFFT are significantly different from those in DeltaNI, try making adjustments to optSensByMertonFFT settings, such as CharacteristicFcnStep, LogStrikeStep, NumFFT, DampingFactor, and so on. Note that if (LogStrikeStep * CharacteristicFcnStep) is 2*pi/ NumFFT, FFT is used. Otherwise, FRFT is used.

Strike = []; % Strike is not specified (will use the entire FFT or FRFT strike grid)
[Delta, Kout] = optSensByMertonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ...
    Sigma, MeanJ, JumpVol, JumpFreq, 'DividendYield', DividendYield, 'OutSpec', "delta", ...
    'NumFFT', NumFFT, 'CharacteristicFcnStep', 0.065, 'LogStrikeStep', 0.001);

% Compare with numerical integration method
Strike = Kout(Range);
DeltaFFT = Delta(Range);
DeltaNI = optSensByMertonNI(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ...
    Sigma, MeanJ, JumpVol, JumpFreq, 'DividendYield', DividendYield, 'OutSpec', "delta");
Error = abs(DeltaFFT-DeltaNI);
table(Strike, DeltaFFT, DeltaNI, Error)

ans=7×4 table
    Strike    DeltaFFT    DeltaNI      Error   
    ______    ________    _______    __________

    79.76     0.53701     0.53701    5.6407e-12
    79.84      0.5341      0.5341    5.3257e-12
    79.92     0.53119     0.53119    5.0099e-12
       80     0.52827     0.52827    4.6956e-12
    80.08     0.52536     0.52536    4.3811e-12
    80.16     0.52245     0.52245    4.0652e-12
    80.24     0.51953     0.51953    3.7503e-12

% Save the final FFT (or FRFT) strike grid for future reference. For
% example, it provides information about the range of Strike inputs for
% which the FFT (or FRFT) operation is valid.
FFTStrikeGrid = Kout;
MinStrike = FFTStrikeGrid(1) % Strike cannot be less than MinStrike

MinStrike = 
47.9437

MaxStrike = FFTStrikeGrid(end) % Strike cannot be greater than MaxStrike

MaxStrike = 
133.3566

Compute the Option Sensitivity for a Single Strike

Once the desired FFT (or FRFT) settings are determined, use the Strike input to specify the strikes rather than providing an empty array. If the specified strikes do not match a value on the FFT (or FRFT) strike grid, the outputs are interpolated on the specified strikes.

Settle = datetime(2017,6,29);
Maturity = datemnth(Settle, 6);
Strike = 80;

Delta = optSensByMertonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ...
    Sigma, MeanJ, JumpVol, JumpFreq, 'DividendYield', DividendYield, 'OutSpec', "delta", ...
    'NumFFT', NumFFT, 'CharacteristicFcnStep', 0.065, 'LogStrikeStep', 0.001)

Delta = 
0.5283

Compute the Option Sensitivities for a Vector of Strikes

Use the Strike input to specify the strikes.

Settle = datetime(2017,6,29);
Maturity = datemnth(Settle, 6);
Strike = (76:2:84)';

Delta = optSensByMertonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ...
    Sigma, MeanJ, JumpVol, JumpFreq, 'DividendYield', DividendYield, 'OutSpec', "delta", ...
    'NumFFT', NumFFT, 'CharacteristicFcnStep', 0.065, 'LogStrikeStep', 0.001)

Delta = 5×1

    0.6727
    0.6013
    0.5283
    0.4565
    0.3883

Compute the Option Sensitivities for a Vector of Strikes and a Vector of Dates of the Same Lengths

Use the Strike input to specify the strikes. Also, the Maturity input can be a vector, but it must match the length of the Strike vector if the ExpandOutput name-value pair argument is not set to "true".

Settle = datetime(2017,6,29);
Maturity = datemnth(Settle, [12 18 24 30 36]); % Five maturities
Strike = [76 78 80 82 84]'; % Five strikes

Delta = optSensByMertonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ...
    Sigma, MeanJ, JumpVol, JumpFreq, 'DividendYield', DividendYield, 'OutSpec', "delta", ...
    'NumFFT', NumFFT, 'CharacteristicFcnStep', 0.065, ...
    'LogStrikeStep', 0.001) % Five values in vector output

Delta = 5×1

    0.6419
    0.5907
    0.5565
    0.5311
    0.5110

Expand the Outputs for a Surface

Set the ExpandOutput name-value pair argument to "true" to expand the outputs into NStrikes-by-NMaturities matrices. In this case, they are square matrices.

[Delta, Kout] = optSensByMertonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ...
    Sigma, MeanJ, JumpVol, JumpFreq, 'DividendYield', DividendYield, 'OutSpec', "delta", ...
    'NumFFT', NumFFT, 'CharacteristicFcnStep', 0.065, ...
    'LogStrikeStep', 0.001, 'ExpandOutput', true) % (5 x 5) matrix output

Delta = 5×5

    0.6419    0.6305    0.6245    0.6204    0.6173
    0.5922    0.5907    0.5905    0.5905    0.5905
    0.5422    0.5507    0.5565    0.5607    0.5637
    0.4927    0.5112    0.5229    0.5311    0.5372
    0.4447    0.4725    0.4898    0.5020    0.5110

Kout = 5×5

    76    76    76    76    76
    78    78    78    78    78
    80    80    80    80    80
    82    82    82    82    82
    84    84    84    84    84

Compute the Option Sensitivities for a Vector of Strikes and a Vector of Dates of Different Lengths

When ExpandOutput is "true", NStrikes do not have to match NMaturities. That is, the output NStrikes-by-NMaturities matrix can be rectangular.

Settle = datetime(2017,6,29);
Maturity = datemnth(Settle, 12*(0.5:0.5:3)'); % Six maturities
Strike = (76:2:84)'; % Five strikes

Delta = optSensByMertonFFT(Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ...
    Sigma, MeanJ, JumpVol, JumpFreq, 'DividendYield', DividendYield, 'OutSpec', "delta", ...
    'NumFFT', NumFFT, 'CharacteristicFcnStep', 0.065, ...
    'LogStrikeStep', 0.001, 'ExpandOutput', true) % (5 x 6) matrix output

Delta = 5×6

    0.6727    0.6419    0.6305    0.6245    0.6204    0.6173
    0.6013    0.5922    0.5907    0.5905    0.5905    0.5905
    0.5283    0.5422    0.5507    0.5565    0.5607    0.5637
    0.4565    0.4927    0.5112    0.5229    0.5311    0.5372
    0.3883    0.4447    0.4725    0.4898    0.5020    0.5110

Compute the Option Sensitivities for a Vector of Strikes and a Vector of Asset Prices

When ExpandOutput is "true", the output can also be a NStrikes-by-NAssetPrices rectangular matrix by accepting a vector of asset prices.

Settle = datetime(2017,6,29);
Maturity = datemnth(Settle, 12); % Single maturity
ManyAssetPrices = [70 75 80 85]; % Four asset prices
Strike = (76:2:84)'; % Five strikes

Delta = optSensByMertonFFT(Rate, ManyAssetPrices, Settle, Maturity, OptSpec, Strike, ...
    Sigma, MeanJ, JumpVol, JumpFreq, 'DividendYield', DividendYield, 'OutSpec', "delta", ...
    'NumFFT', NumFFT, 'CharacteristicFcnStep', 0.065, ...
    'LogStrikeStep', 0.001, 'ExpandOutput', true) % (5 x 4) matrix output

Delta = 5×4

    0.3796    0.5157    0.6419    0.7472
    0.3315    0.4637    0.5922    0.7043
    0.2874    0.4137    0.5422    0.6592
    0.2474    0.3664    0.4927    0.6128
    0.2117    0.3224    0.4447    0.5657

Plot Option Sensitivity Surfaces

Use the Strike input to specify the strikes. Increase the value for NumFFT to support a wider range of strikes. Also, the Maturity input can be a vector. Set ExpandOutput to "true" to output the surfaces as NStrikes-by-NMaturities matrices.

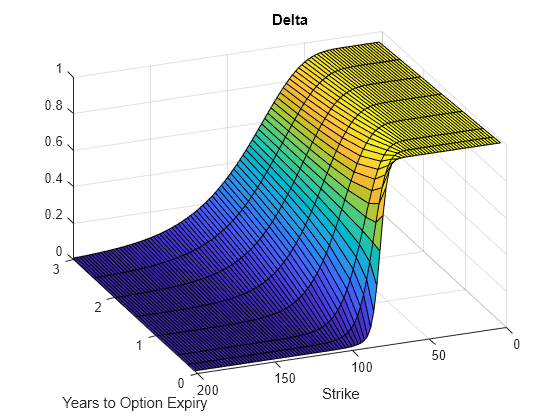
Settle = datetime(2017,6,29);
Maturity = datemnth(Settle, 12*[1/12 0.25 (0.5:0.5:3)]');
Times = yearfrac(Settle, Maturity);
Strike = (2:2:200)';

% Increase 'NumFFT' to support a wider range of strikes
NumFFT = 2^13;

[Delta, Gamma, Rho, Theta, Vega] = optSensByMertonFFT(...
    Rate, AssetPrice, Settle, Maturity, OptSpec, Strike, ...
    Sigma, MeanJ, JumpVol, JumpFreq, 'DividendYield', DividendYield, ...
    'NumFFT', NumFFT, 'CharacteristicFcnStep', 0.065, 'LogStrikeStep', 0.001, ...
    'OutSpec', ["delta", "gamma", "rho", "theta", "vega"], ...
    'ExpandOutput', true);

[X,Y] = meshgrid(Times,Strike);

figure;
surf(X,Y,Delta);
title('Delta');
xlabel('Years to Option Expiry');
ylabel('Strike');
view(-112,34);
xlim([0 Times(end)]);

figure;
surf(X,Y,Gamma)
title('Gamma')
xlabel('Years to Option Expiry')
ylabel('Strike')
view(-112,34);
xlim([0 Times(end)]);

figure;
surf(X,Y,Rho)
title('Rho')
xlabel('Years to Option Expiry')
ylabel('Strike')
view(-112,34);
xlim([0 Times(end)]);

figure;
surf(X,Y,Theta)
title('Theta')
xlabel('Years to Option Expiry')
ylabel('Strike')
view(-112,34);
xlim([0 Times(end)]);

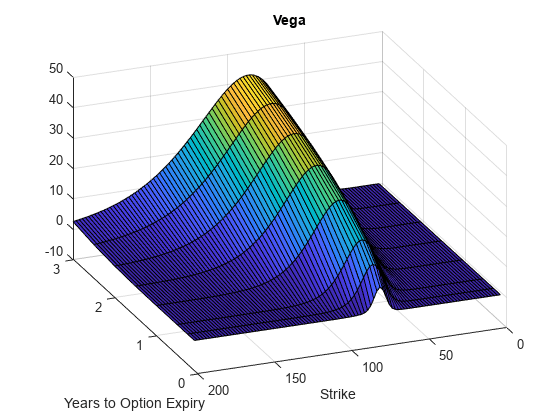
figure;
surf(X,Y,Vega)
title('Vega')
xlabel('Years to Option Expiry')
ylabel('Strike')
view(-112,34);
xlim([0 Times(end)]);

Input Arguments

Rate — Continuously compounded risk-free interest rate

decimal

Continuously compounded risk-free interest rate, specified as a scalar decimal value.

Data Types: double

AssetPrice — Current underlying asset price

numeric

Current underlying asset price, specified as numeric value using a scalar or a NINST-by-1 or NColumns-by-1 vector.

For more information on the proper dimensions for AssetPrice, see the name-value pair argument ExpandOutput.

Data Types: double

Settle — Option settlement date

datetime array | string array | date character vector

Option settlement date, specified as a NINST-by-1 or NColumns-by-1 vector using a datetime array, string array, or date character vectors. The Settle date must be before the Maturity date.

To support existing code, optSensByMertonFFT also accepts serial date numbers as inputs, but they are not recommended.

For more information on the proper dimensions for Settle, see the name-value pair argument ExpandOutput.

Maturity — Option maturity date

datetime array | string array | date character vector

Option maturity date, specified as a NINST-by-1 or NColumns-by-1 vector using a datetime array, string array, or date character vectors.

To support existing code, optSensByMertonFFT also accepts serial date numbers as inputs, but they are not recommended.

For more information on the proper dimensions for Maturity, see the name-value pair argument ExpandOutput.

OptSpec — Definition of option

cell array of character vector with values 'call' or 'put' | string array with values "call" or "put"

Definition of the option, specified as a NINST-by-1 or NColumns-by-1 vector using a cell array of character vectors or string arrays with values 'call' or 'put'.

For more information on the proper dimensions for OptSpec, see the name-value pair argument ExpandOutput.

Data Types: cell | string

Strike — Option strike price value

numeric

Option strike price value, specified as a NINST-by-1, NRows-by-1, NRows-by-NColumns vector of strike prices.

If this input is an empty array ([]), option prices are computed on the entire FFT (or FRFT) strike grid, which is determined as exp(log-strike grid). Each column of the log-strike grid has'NumFFT' points with 'LogStrikeStep' spacing that are roughly centered around each element of log(AssetPrice).

For more information on the proper dimensions for Strike, see the name-value pair argument ExpandOutput.

Data Types: double

Sigma — Volatility of underlying asset

numeric

Volatility of the underlying asset, specified as a scalar numeric value.

Data Types: double

MeanJ — Mean of the random percentage jump size

decimal

Mean of the random percentage jump size (J), specified as a scalar decimal value where log(1+J) is normally distributed with mean (log(1+MeanJ)-0.5*JumpVol^2) and the standard deviation JumpVol.

Data Types: double

JumpVol — Standard deviation of log(1+J)

decimal

Standard deviation of log(1+J) where J is the random percentage jump size, specified as a scalar decimal value.

Data Types: double

JumpFreq — Annual frequency of Poisson jump process

numeric

Annual frequency of Poisson jump process, specified as a scalar numeric value.

Data Types: double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: [PriceSens,StrikeOut] = optSensByMertonFFT(Rate,AssetPrice,Settle,Maturity,OptSpec,Strike,Sigma,MeanJ,JumpVol,JumpFreq,'Basis',7)

Basis — Day-count basis of instrument

0 (default) | numeric values: 0,1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 13

Day-count of the instrument, specified as the comma-separated pair consisting of 'Basis' and a scalar using a supported value:

• 0 = actual/actual

• 1 = 30/360 (SIA)

• 2 = actual/360

• 3 = actual/365

• 4 = 30/360 (PSA)

• 5 = 30/360 (ISDA)

• 6 = 30/360 (European)

• 7 = actual/365 (Japanese)

• 8 = actual/actual (ICMA)

• 9 = actual/360 (ICMA)

• 10 = actual/365 (ICMA)

• 11 = 30/360E (ICMA)

• 12 = actual/365 (ISDA)

• 13 = BUS/252

For more information, see Basis.

Data Types: double

DividendYield — Continuously compounded underlying asset yield

0 (default) | numeric

Continuously compounded underlying asset yield, specified as the comma-separated pair consisting of 'DividendYield' and a scalar numeric value.

Data Types: double

OutSpec — Define outputs

["price"] (default) | string array with values "price", "delta", "gamma", "vega", "rho", and "theta" | cell array of character vectors with values 'price', 'delta', 'gamma', 'vega', 'rho', and 'theta'

Define outputs, specified as the comma-separated pair consisting of 'OutSpec' and a NOUT- by-1 or a 1-by-NOUT string array or cell array of character vectors with supported values.

Note

"vega" is the sensitivity with respect the initial volatility sqrt(V0).

Example: OutSpec = ["price","delta","gamma","vega","rho","theta"]

Data Types: string | cell

NumFFT — Number of grid points in the characteristic function variable

4096 (default) | numeric

Number of grid points in the characteristic function variable and in each column of the log-strike grid, specified as the comma-separated pair consisting of 'NumFFT' and a scalar numeric value.

Data Types: double

CharacteristicFcnStep — Characteristic function variable grid spacing

0.01 (default) | numeric

Characteristic function variable grid spacing, specified as the comma-separated pair consisting of 'CharacteristicFcnStep' and a scalar numeric value.

Data Types: double

LogStrikeStep — Log-strike grid spacing

2*pi/NumFFT/CharacteristicFcnStep (default) | numeric

Log-strike grid spacing, specified as the comma-separated pair consisting of 'LogStrikeStep' and a scalar numeric value.

Note

If (LogStrikeStep*CharacteristicFcnStep) is 2*pi/NumFFT, FFT is used. Otherwise, FRFT is used.

Data Types: double

DampingFactor — Damping factor for Carr-Madan formulation

1.5 (default) | numeric

Damping factor for Carr-Madan formulation, specified as the comma-separated pair consisting of 'DampingFactor' and a scalar numeric value.

Data Types: double

Quadrature — Type of quadrature

"simpson" (default) | character vector with values:'simpson' or 'trapezoidal' | string array with values: "simpson" or "trapezoidal"

Type of quadrature, specified as the comma-separated pair consisting of 'Quadrature' and a single character vector or string array with a value of 'simpson' or 'trapezoidal'.

Data Types: char | string

ExpandOutput — Flag to expand the outputs

false (outputs are NINST-by-1 vectors) (default) | logical with value of true or false

Flag to expand the outputs, specified as the comma-separated pair consisting of 'ExpandOutput' and a logical:

• true — If true, the outputs are NRows-by- NColumns matrices. NRows is the number of strikes for each column and it is determined by the Strike input. For example, Strike can be a NRows-by-1 vector, or a NRows-by-NColumns matrix. If Strike is empty, NRows is equal to NumFFT. NColumns is determined by the sizes of AssetPrice, Settle, Maturity, and OptSpec, which must all be either scalar or NColumns-by-1 vectors.

• false — If false, the outputs are NINST-by-1 vectors. Also, the inputs Strike, AssetPrice, Settle, Maturity, and OptSpec must all be either scalar or NINST-by-1 vectors.

Data Types: logical

Output Arguments

PriceSens — Option prices or sensitivities

numeric

Option prices or sensitivities, returned as a NINST-by-1, or NRows-by-NColumns, depending on ExpandOutput. The name-value pair argument OutSpec determines the types and order of the outputs.

StrikeOut — Strikes corresponding to Price

numeric

Strikes corresponding to Price, returned as a NINST-by-1, or NRows-by-NColumns, depending on ExpandOutput.

More About

Vanilla Option

A vanilla option is a category of options that includes only the most standard components.

A vanilla option has an expiration date and straightforward strike price. American-style options and European-style options are both categorized as vanilla options.

The payoff for a vanilla option is as follows:

• For a call: $$\max (St-K,0)$$

• For a put: $$\max (K-St,0)$$

where:

St is the price of the underlying asset at time t.

K is the strike price.

For more information, see Vanilla Option.

Merton Jump Diffusion Model

The Merton jump diffusion model (Merton (1976)) is a different extension of the Black-Scholes model, where sudden asset price movements (both up and down) are modeled by adding the jump diffusion parameters with the Poisson process.

The stochastic differential equation is:

$$\begin{array}{l}d{S}_t=(r-q-{\lambda }_p{\mu }_j)S_{t}dt+\sigma S_{t}d{W}_t+J{S}_{t}d{P}_t\\ \text{prob(}d{P}_t=1)={\lambda }_{p}dt\end{array}$$

where

r is the continuous risk-free rate.

q is the continuous dividend yield.

W_t is the Wiener process.

J is the random percentage jump size conditional on the jump occurring, where ln(1+J) is normally distributed with mean $$\ln (1+{\mu }_J)-\frac{{\delta }^2}{2}$$ and the standard deviation δ, and (1+J) has a lognormal distribution:

$$\frac{1}{(1+J)\delta \sqrt{2\pi }}\exp \left\{{\frac{-\left[\ln (1+J)-\left(\ln (1+{\mu }_J\right)-\frac{{\delta }^2}{2}\right]}{2{\delta }^2}}^2\right\}$$

μ_J is the mean of J for (μ_J > -1).

δ is the standard deviation of ln(1+J) for (δ≥ 0).

ƛ_p is the annual frequency (intensity) of Poisson process P_tfor (ƛ_p ≥ 0).

σ is the volatility of the asset price for (σ > 0).

The characteristic function $$f_{Merton{76}_j}(\varphi )$$ for j = 1 (asset prices measure) and j = 2 (risk-neutral measure) is:

$$\begin{array}{l}{f}_{Merton{76}_j}=f_{B{S}_j}\exp \left({\lambda }_p\tau {\left(1+{\mu }_j\right)}^{m_j+\frac{1}{2}}\left[{\left(1+{\mu }_j\right)}^{i\varphi }{e}^{{\delta }^2\left(m_{j}i\varphi +\frac{{(i\varphi )}^2}{2}\right)}-1\right]-{\lambda }_p\tau {\mu }_{j}i\varphi \right)\\ \text{where for }j=1,2:\\ f_{B{S}_1}(\varphi )=\frac{f_{B{S}_2}\left(\varphi -i\right)}{f_{B{S}_2}\left(-i\right)}\\ f_{BS2}(\varphi )=\exp \left(i\varphi \left[\ln S_t+\left(r-q-\frac{{\sigma }^2}{2}\right)\tau \right]-\frac{{\varphi }^2{\sigma }^2}{2}\tau \right)\\ m_1=\frac{1}{2},m_2=-\frac{1}{2}\end{array}$$

where

ϕ is the characteristic function variable.

τ is the time to maturity (τ = T- t).

i is the unit imaginary number ( i² = -1).

Carr-Madan Formulation

The Carr and Madan (1999) formulation is a popular modified implementation of Heston (1993) framework.

Rather than computing the probabilities P₁ and P₂ as intermediate steps, Carr and Madan developed an alternative expression so that taking its inverse Fourier transform gives the option price itself directly.

$$\begin{array}{l}Call(k)=\frac{e^{-\alpha k}}{\pi }{\displaystyle {\int }_0^{\infty }\mathrm{Re}\left[e^{-iuk}\psi (u)\right]}du\\ \psi (u)=\frac{e^{-r\tau }{f}_2(\varphi =(u-(\alpha +1)i))}{{\alpha }^2+\alpha -u^2+iu(2\alpha +1)}\\ Put(K)=Call(K)+K{e}^{-r\tau }-S_t{e}^{-q\tau }\end{array}$$

where

r is the continuous risk-free rate.

q is the continuous dividend yield.

S_t is the asset price at time t.

τ is time to maturity (τ = T-t).

Call(K) is the call price at strike K.

Put(K) is the put price at strike K.

i is a unit imaginary number (i²= -1).

ϕ is the characteristic function variable.

α is the damping factor.

u is the characteristic function variable for integration, where ϕ = (u - (α+1)i).

f₂(ϕ) is the characteristic function for P₂.

P₂ is the probability of S_t > K under the risk-neutral measure for the model.

To apply FFT or FRFT to this formulation, the characteristic function variable for integration, u, is discretized into NumFFT(N) point with the step size CharacteristicFcnStep (Δu), and the log-strike k is discretized into N points with the step size LogStrikeStep(Δk).

The discretized characteristic function variable for integration, u_j(for j = 1,2,3,…,N), has a minimum value of 0 and a maximum value of (N-1) (Δu), and it approximates the continuous integration range from 0 to infinity.

The discretized log-strike grid, k_n(for n = 1, 2, 3, N) is approximately centered around ln(S_t), with a minimum value of

$$\ln (S_t)-\frac{N}{2}\Delta k$$

and a maximum value of

$$\ln (S_t)+\left(\frac{N}{2}-1\right)\Delta k$$

Where the minimum allowable strike is

$$S_t\exp \left(-\frac{N}{2}\Delta k\right)$$

and the maximum allowable strike is

$$S_t\exp \left[\left(\frac{N}{2}-1\right)\Delta k\right]$$

As a result of the discretization, the expression for the call option becomes

$$Call(k_n)=\Delta u\frac{e^{-\alpha k_n}}{\pi }{\displaystyle \sum _{j=1}^N\mathrm{Re}\left[e^{-i\Delta k\Delta u(j-1)(n-1)e^{i{u}_j}\left[\frac{N\Delta k}{2}-\ln (S_t)\right]}\psi (u_j)\right]}{w}_j$$

where

Δu is the step size of discretized characteristic function variable for integration.

Δk is the step size of discretized log-strike.

N is the number of FFT or FRFT points.

w_j is the weights for quadrature used for approximating the integral.

FFT is used to evaluate the above expression if Δk and Δu are subject to the following constraint:

$$\Delta k\Delta u=\left(\frac{2\pi }{N}\right)$$

otherwise, the functions use the FRFT method described in Chourdakis (2005).

References

[1] Bates, D. S. “Jumps and Stochastic Volatility: Exchange Rate Processes Implicit in Deutsche Mark Options.” The Review of Financial Studies. Vol 9. No. 1. 1996.

[2] Carr, P., and D.B. Madan. “Option Valuation Using the Fast Fourier Transform.” Journal of Computational Finance. Vol 2. No. 4. 1999.

[3] Cont, R. and P. Tankov. Financial Modeling with Jump Processes. Chapman & Hall/CRC Press, 2004.

[4] Chourdakis, K. “Option Pricing Using Fractional FFT.” Journal of Computational Finance. 2005.

[5] Merton, R. “Option Pricing When Underlying Stock Returns are Discontinuous.” Journal of Financial Economics. Vol 3. 1976.

Version History

Introduced in R2018a

R2022b: Serial date numbers not recommended

Although optSensByMertonFFT supports serial date numbers, datetime values are recommended instead. The datetime data type provides flexible date and time formats, storage out to nanosecond precision, and properties to account for time zones and daylight saving time.

To convert serial date numbers or text to datetime values, use the datetime function. For example:

t = datetime(738427.656845093,"ConvertFrom","datenum");
y = year(t)

y =

        2021

There are no plans to remove support for serial date number inputs.