Create PAC and Sequential CMO

This example shows how to use an underlying mortgage-backed security (MBS) pool to define a PAC bond, and then define a sequential CMO from the PAC bond. Specifically, this example uses a 30-year fixed-rate mortgage of 6% to define a PAC bond, and then define a sequential CMO from the PAC bond. You can analyze the CMO by comparing the CMO spread to a zero-rate curve for a 30-year Treasury bond and then calculate the weighted-average life (WAL) for the PAC bond.

Define Underlying Mortgage Pool

principal = 100000000;
grossrate = 0.06;
coupon = 0.05;
originalTerm = 360;
termRemaining = 360;
speed = 100;
delay = 14;

Settle      = datenum('1-Jan-2011');
IssueDate   = datenum('1-Jan-2011');
Maturity    = addtodate(IssueDate, 360, 'month');

Calculate Underlying Pool Cash Flow

Use mbscfamounts to calaculate the cash flow for the mortgage pool.

[CFlowAmounts, CFlowDates, ~, ~, ~, UnitPrincipal, UnitInterest, ...
UnitPrepayment] = mbscfamounts(Settle, Maturity, IssueDate, grossrate, ...
coupon, delay, speed, []);

Calculate Prepayments

principalPayments = UnitPrincipal * principal;
netInterest = UnitInterest * principal;
prepayments = UnitPrepayment * principal;
dates = CFlowDates' + delay;

Generate Plot for Underlying MBS Payments

area([principalPayments'+prepayments', netInterest'])
title('Underlying MBS Payments');
legend('Principal Payments (incl. Prepayments)', 'Interest Payments')

Calculate PAC Schedule

Use cmosched to generate the principal balance schedule for the PAC.

pacSpeed = [80 300];
[balanceSchedule, pacInitBalance] = ...
cmosched(principal, grossrate, originalTerm, termRemaining, ...
pacSpeed, []);

Generate Plot for PAC Principal Balance Schedule

figure;
area([pacInitBalance'; balanceSchedule'])
title('PAC Principal Balance Schedule');
legend('Principal Balance Schedule');

Calculate PAC Cash Flow

Use cmoschedcf to generate cash flows for scheduled collateralized mortgage obligation (CMO) using a PAC model.

pacTranchePrincipals = [pacInitBalance; principal-pacInitBalance];
pacTrancheCoupons = [0.05; 0.05];
[pacBalances, pacPrincipals, pacInterests] = ...
cmoschedcf(principalPayments+prepayments, ...
pacTranchePrincipals, pacTrancheCoupons, balanceSchedule);

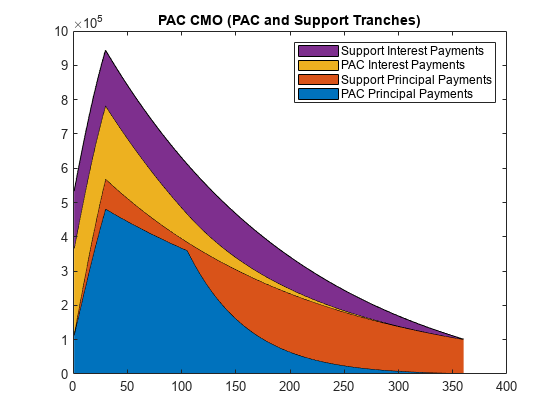
Generate Plot for PAC CMO Tranches

Generate a plot for the PAC CMO tranches:

figure;
area([pacPrincipals' pacInterests']);
title('PAC CMO (PAC and Support Tranches)');
legend('PAC Principal Payments', 'Support Principal Payments', ...
'PAC Interest Payments', 'Support Interest Payments');

Create Sequential CMO from PAC Bond

Create CMO tranches, A, B, C, and D.

seqTranchePrincipals = ...
[20000000; 20000000; 10000000; pacInitBalance-50000000];
seqTrancheCoupons = [0.05; 0.05; 0.05; 0.05];

Calculate Cash Flows for Each Tranche

[seqBalances, seqPrincipals, seqInterests] = ...
cmoseqcf(pacPrincipals(1, :), seqTranchePrincipals, ...
seqTrancheCoupons, false);

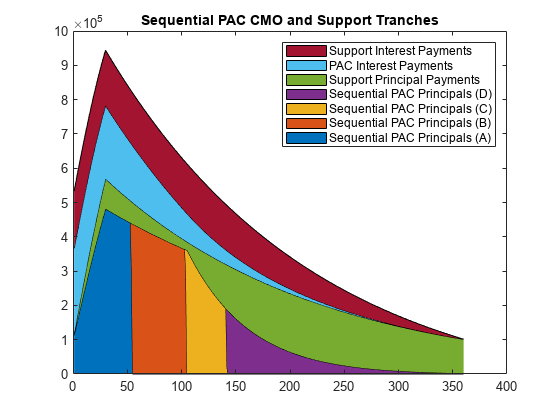
Generate Plot for Sequential PAC CMO

Generate a plot for the sequential PAC CMO.

figure
area([seqPrincipals' pacPrincipals(2, :)' pacInterests']);
title('Sequential PAC CMO and Support Tranches');
legend('Sequential PAC Principals (A)', 'Sequential PAC Principals (B)', ...
'Sequential PAC Principals (C)', 'Sequential PAC Principals (D)', ...
'Support Principal Payments', 'PAC Interest Payments', ...
'Support Interest Payments');

Create Discount Curve

Use intenvset to create zeroCurve.

CurveSettle = datenum('1-Jan-2011');
ZeroRates = [0.01 0.03 0.10 0.19 0.45 0.81 1.76 2.50 3.18 4.09 4.38]'/100;
CurveTimes = [1/12 3/12 6/12 1 2 3 5 7 10 20 30]';
CurveDates = daysadd(CurveSettle, 360 * CurveTimes, 1);
zeroCurve = intenvset('Rates', ZeroRates, 'StartDates', CurveSettle, ...
'EndDates', CurveDates);

Price CMO Cash Flows

The cash flow for the sequential PAC principal A tranche is calculated using the cash flow functions cfbyzero, cfyield, cfprice, and cfspread.

cflows = seqPrincipals(1, :)+seqInterests(1, :);
cfdates = dates(2:end)';
price1 = cfbyzero(zeroCurve, cflows, cfdates, Settle, 4)

price1 = 
2.2109e+07

yield = cfyield(cflows, cfdates, price1, Settle, 'Basis', 4)

yield = 
0.0090

price2 = cfprice(cflows, cfdates, yield, Settle, 'Basis', 4)

price2 = 
2.2109e+07

spread = cfspread(zeroCurve, price2, cflows, cfdates, Settle, 'Basis', 4)

spread = 
5.5084e-12

WAL = sum(cflows .* yearfrac(Settle, cfdates, 4)) / sum(cflows)

WAL = 
2.5408

The weighted average life (WAL) for the sequential PAC principal A tranche is 2.54 years.