Transform Time Series Using Econometric Modeler App
The Econometric Modeler app enables you to transform time series data based on deterministic or stochastic trends you see in plots or hypothesis test conclusions. Available transformations in the app are log, seasonal and nonseasonal difference, and linear detrend. These examples show how to apply each transformation to time series data.
Apply Log Transformation to Data
This example shows how to stabilize a time series, whose
variability grows with the level of the series, by applying the log
transformation. The data set Data_Airline.mat contains monthly counts of airline passengers.
At the command line, load the Data_Airline.mat data set.
load Data_AirlineAt the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
Import DataTimeTable into the app:
On the Econometric Modeler tab, in the Import section, click the Import button
 .
.In the Import Data dialog box, in the Import? column, select the check box for the
DataTimeTablevariable.Click Import.
The variable PSSG appears in the Time
Series pane, and its time series plot is in the
Time Series Plot(PSSG) figure window.
Fit a SARIMA(0,1,1)×(0,1,1)12 model to the data in levels:
On the Econometric Modeler tab, in the Models section, click the arrow to display the model gallery.
In the models gallery, in the ARMA/ARIMA Models section, click SARIMA.
In the SARIMA Model Parameters dialog box, on the Lag Order tab:
Nonseasonal section
Set Degrees of Integration to
1.Set Moving Average Order to
1.Clear the Include Constant Term check box.
Seasonal section
Set Period to
12to indicate monthly data.Set Moving Average Order to
1.Select the Include Seasonal Difference check box.

Click Estimate.
The model variable SARIMA_PSSG appears in the
Models pane, its value appears in the
Preview pane, and its estimation summary appears in
the Model Summary(SARIMA_PSSG) document.

The spread of the residuals increases with the level of the data, which is indicative of heteroscedasticity.
Apply the log transform to PSSG:
In the Time Series pane, select
PSSG.On the Econometric Modeler tab, in the Transforms section, click Log.
The transformed variable PSSGLog appears in the Time Series pane, and its time series plot appears in the Time Series Plot(PSSGLog) figure window.
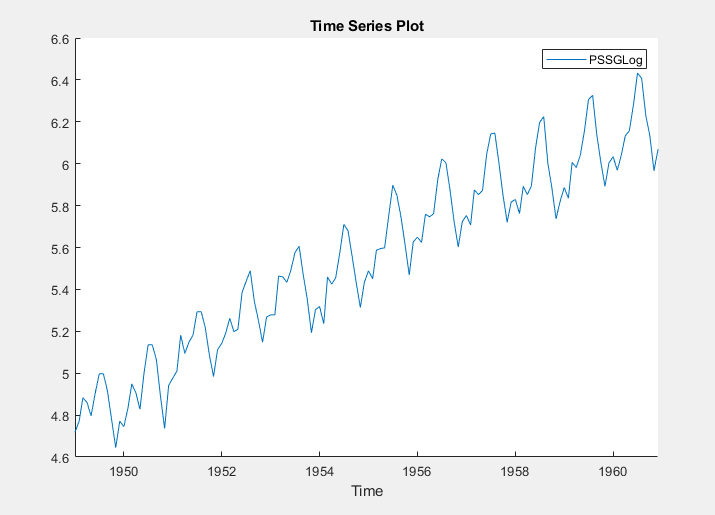
The exponential growth appears removed from the series.
With PSSGLog selected in the Time
Series pane, fit the
SARIMA(0,1,1)×(0,1,1)12 model to the logged
series using the same dialog box settings that you used for
PSSG. The estimation summary appears in the
Model Summary(SARIMA_PSSGLog) document.
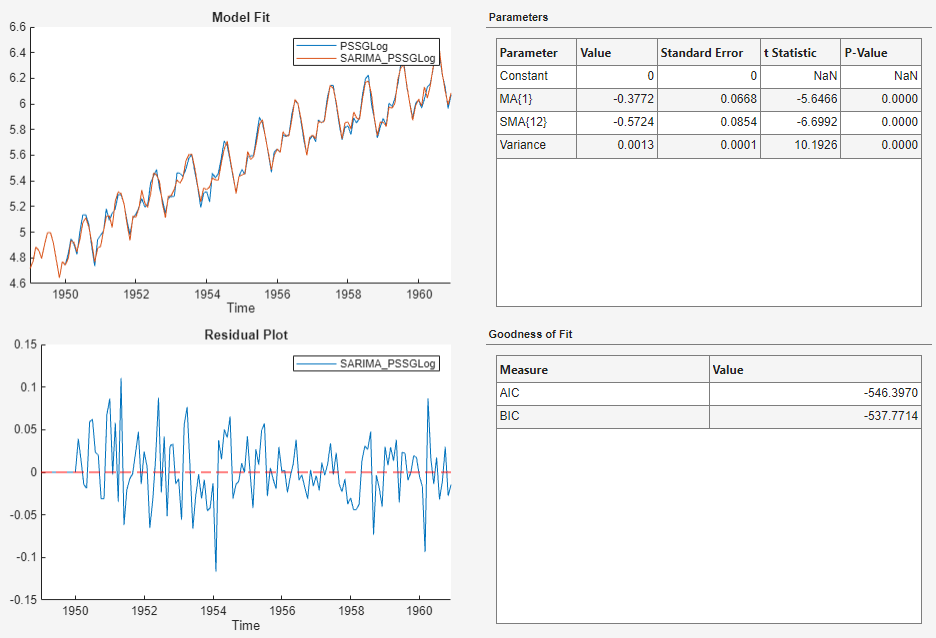
The spread of the residuals does not appear to change systematically with the levels of the data.
Stabilize Time Series Using Nonseasonal Differencing
This example shows how to stabilize a time series by applying
multiple nonseasonal difference operations. The data set, which is stored in
Data_USEconModel.mat, contains the US gross domestic
product (GDP) measured quarterly, among other series.
At the command line, load the Data_USEconModel.mat data
set.
load Data_USEconModelAt the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
Import DataTimeTable into the app:
On the Econometric Modeler tab, in the Import section, click the Import button
 .
.In the Import Data dialog box, in the Import? column, select the check box for the
DataTimeTablevariable.Click Import.
The variables, including GDP, appear in the
Time Series pane, and a time series plot of all the
series appears in the Time Series Plot(COE) figure
window.
In the Time Series pane, double-click
GDP. A time series plot of
GDP appears in the Time Series
Plot(GDP) figure window.

The series appears to grow without bound.
Apply the first difference to GDP. On the
Econometric Modeler tab, in the
Transforms section, click
Difference.
In the Time Series pane, a variable representing the
differenced GDP (GDPDiff) appears. A time series
plot of the differenced GDP appears in the Time Series
Plot(GDPDiff) figure window.
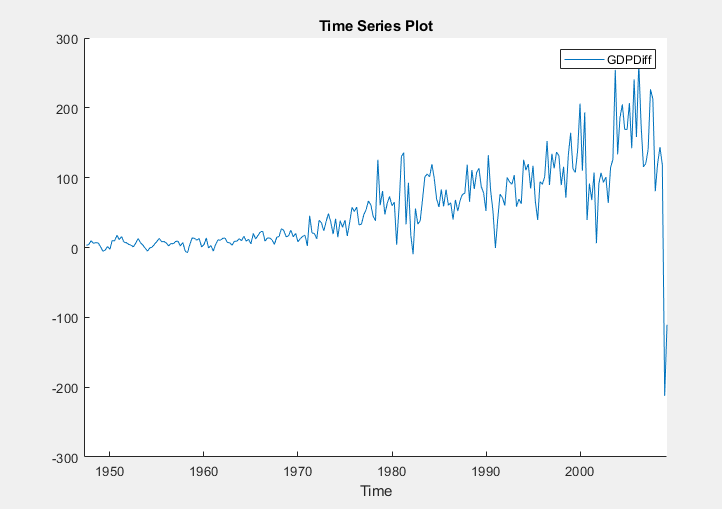
The differenced GDP series appears to grow without bound after 1970.
Apply the second difference to the GDP by differencing the differenced
GDP. With GDPDiff selected in the Time
Series pane, on the Econometric Modeler
tab, in the Transforms section, click
Difference.
In the Time Series pane, a variable representing the
transformed differenced GDP (GDPDiffDiff)
appears. A time series plot of the differenced GDP appears in the
Time Series Plot(GDPDiffDiff) figure window.
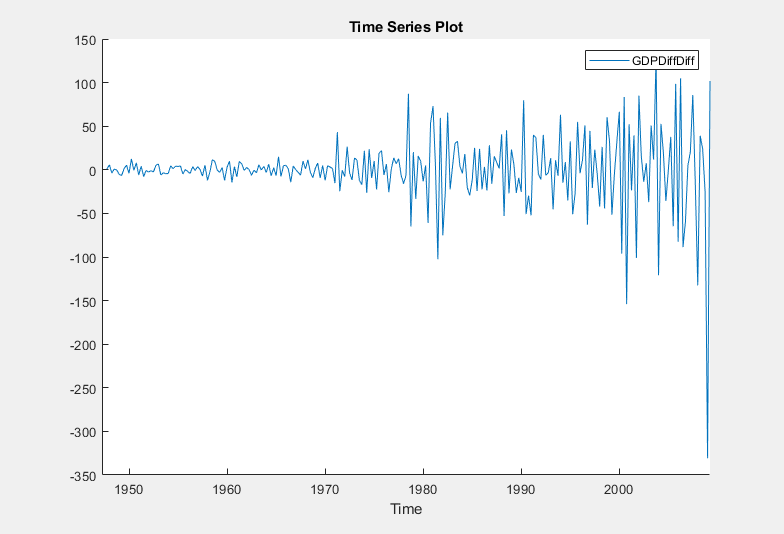
The transformed differenced GDP series appears stationary, although heteroscedastic.
Convert Prices to Returns
This example shows how to convert multiple series of prices
to returns. The data set, which is stored in
Data_USEconModel.mat, contains the US GDP and personal
consumption expenditures measured quarterly, among other series.
At the command line, load the Data_USEconModel.mat data
set.
load Data_USEconModelAt the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
Import DataTimeTable into the app:
On the Econometric Modeler tab, in the Import section, click the Import button
 .
.In the Import Data dialog box, in the Import? column, select the check box for the
DataTimeTablevariable.Click Import.
GDP and PCEC, among
other series, appear in the Time Series pane, and a
time series plot containing all series appears in the figure window.
In the Time Series pane, click
GDP, then press Ctrl and
click PCEC. Both series are selected.
Click the Plots tab, then click Time
Series. A time series plot of GDP
and PCEC appears in the Time Series
Plot(GDP) figure window.
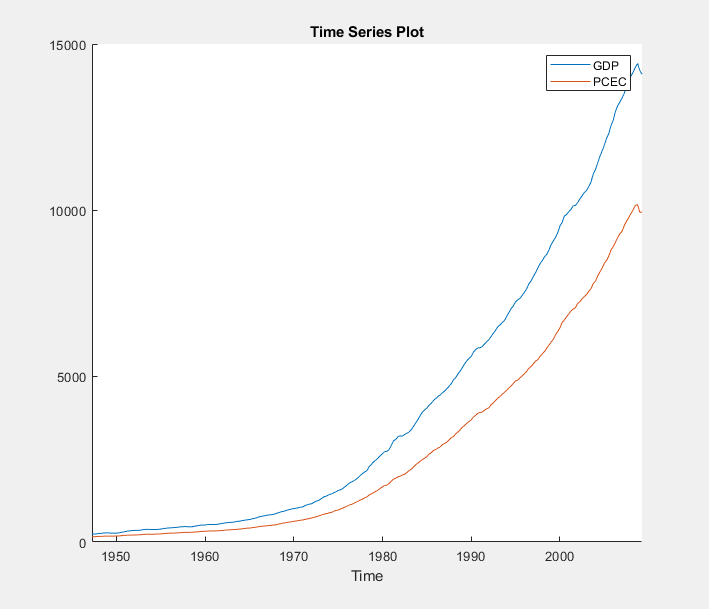
Both series, as prices, appear to grow without bound.
Convert the GDP and personal consumption expenditure prices to returns:
Click the Econometric Modeler tab. Ensure that
GDPandPCECare selected in the Time Series pane.In the Transforms section, click Log.
The Time Series pane displays variables representing the logged GDP series (
GDPLog) and the logged personal consumption expenditure series (PCECLog).With
GDPLogandPCECLogselected in the Time Series pane, in the Transforms section, click Difference.
The Time Series pane displays variables representing
the GDP returns (GDPLogDiff) and personal
consumption expenditure returns (PCECLogDiff). A
time series plot of the GDP and personal consumption expenditure returns
appears in the Time Series Plot(GDPLogDiff) figure
window.
In the Time Series pane, rename the
GDPLogDiff and
PCECLogDiff variables. Click
GDPLogDiff twice to select its name and enter
GDPReturns. Click
PCECLogDiff twice to select its name and
enter PCECReturns.
The app updates the names of all documents associated with both returns.
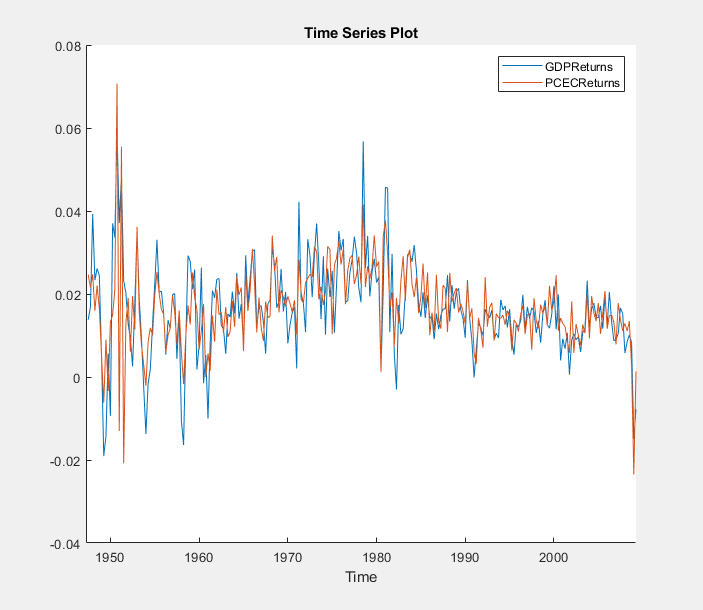
The series of GDP and personal consumption expenditure returns appear stationary, but observations within each series appear serially correlated.
Remove Seasonal Trend from Time Series Using Seasonal Difference
This example shows how to stabilize a time series exhibiting
seasonal integration by applying a seasonal difference. The data set Data_Airline.mat contains monthly counts of airline passengers.
At the command line, load the Data_Airline.mat data set.
load Data_AirlineAt the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
Import DataTimeTable into the app:
On the Econometric Modeler tab, in the Import section, click the Import button
 .
.In the Import Data dialog box, in the Import? column, select the check box for the
DataTimeTablevariable.Click Import.
The variable PSSG appears in the Time
Series pane, and its time series plot appears in the
Time Series Plot(PSSG) figure window.
Address the seasonal trend by applying the 12th order seasonal difference.
On the Econometric Modeler tab, in the
Transforms section, set
Seasonal to 12. Then, click
Seasonal.
The transformed variable PSSGSeasonalDiff
appears in the Time Series pane, and its time series
plot appears in the Time Series Plot(PSSGSeasonalDiff)
figure window.
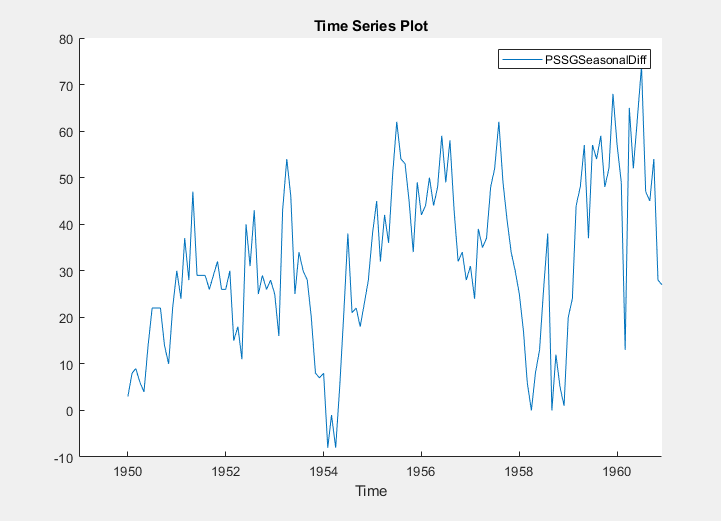
The transformed series appears to have a nonseasonal trend.
Address the nonseasonal trend by applying the first difference. With
PSSGSeasonalDiff selected in the
Time Series pane, on the Econometric
Modeler tab, in the Transforms section,
click Difference.
The transformed variable PSSGSeasonalDiffDiff
appears in the Time Series pane, and its time series
plot appears in the Time Series
Plot(PSSGSeasonalDiffDiff) figure window.
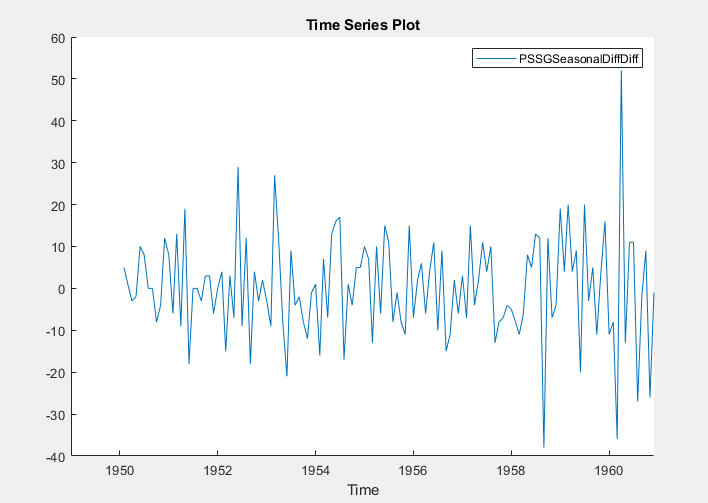
The transformed series appears stationary, but observations appear serially correlated.
In the Time Series pane, rename the
PSSGSeasonalDiffDiff variable by clicking it
twice to select its name and entering
PSSGStable.
The app updates the names of all documents associated with the transformed series.
Remove Deterministic Trend from Time Series
This example shows how to remove a least-squares-derived
deterministic trend from a nonstationary time series. The data set Data_Airline.mat contains monthly counts of airline passengers.
At the command line, load the Data_Airline.mat data set.
load Data_AirlineAt the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
Import DataTimeTable into the app:
On the Econometric Modeler tab, in the Import section, click the Import button
 .
.In the Import Data dialog box, in the Import? column, select the check box for the
DataTimeTablevariable.Click Import.
The variable PSSG appears in the Time
Series pane, and its time series plot appears in the
Time Series Plot(PSSG) figure window.
Apply the log transformation to the series. On the Econometric Modeler tab, in the Transforms section, click Log.
The transformed variable PSSGLog appears in the
Time Series pane, and its time series plot appears
in the Time Series Plot(PSSGLog) figure window.
Identify the deterministic trend by using least squares. Then, detrend the series by removing the identified deterministic trend. On the Econometric Modeler tab, in the Transforms section, click Detrend.
The transformed variable PSSGLogDetrend appears
in the Time Series pane, and its time series plot
appears in the Time Series Plot(PSSGLogDetrend) figure
window.

PSSGLogDetrend does not appear to have a
deterministic trend, although it has a marked cyclic trend.