Simulate Univariate Markov-Switching Dynamic Regression Model

This example shows how to generate random response and state paths from a two-state Markov-switching dynamic regression model.

Suppose that an economy switches between two regimes: an expansion and a recession. If the economy is in an expansion, the probability that the expansion persists in the next time step is 0.9, and the probability that it switches to a recession is 0.1. If the economy is in a recession, the probability that the recession persists in the next time step is 0.7, and the probability that it switches to a recession is 0.3.

$$P=\left[\begin{array}{cc}0.9& 0.1\\ 0.3& 0.7\end{array}\right].$$

Also suppose that ${\mathit{y}}_{\mathit{t}}$ is a univariate response process representing an economic measurement that can suggest which state the economy experiences during a period. During an expansion, ${\mathit{y}}_{\mathit{t}}$ is this AR(2) model:

$$y_t=5+0.3y_{t-1}+0.2y_{t-2}+{\epsilon }_{1t},$$

where ${\epsilon }_{1\mathit{t}}$ is an iid Gaussian process with mean 0 and variance 2. During a recession, ${\mathit{y}}_{\mathit{t}}$ is this AR(1) model:

$$y_t=-5+0.1y_{t-1}+{\epsilon }_{2t},$$

where ${\epsilon }_{2\mathit{t}}$ is an iid Gaussian process with mean 0 and variance 1.

Create Fully Specified Model

Create the Markov-switching dynamic regression model that describes the state of the economy with respect to ${\mathit{y}}_{\mathit{t}}$.

% Switching mechanism
P = [0.9 0.1; 0.3 0.7];
mc = dtmc(P,StateNames=["Expansion" "Recession"]);

% AR submodels 
mdl1 = arima(Constant=5,AR=[0.3 0.2],Variance=2, ...
    Description="Expansion State");
mdl2 = arima(Constant=-5,AR=0.1,Variance=1, ...
    Description="Recession State");

% Markov-switching model
Mdl = msVAR(mc,[mdl1; mdl2]);

Mdl is a fully specified msVAR object.

Simulate One Path

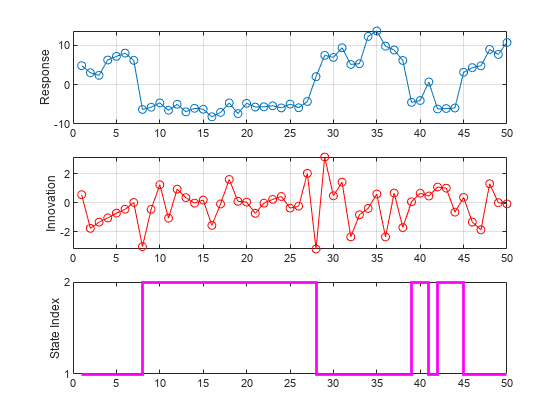
Simulate one path of responses, innovations, and state indices from the model. Specify a 50-period simulation horizon, that is, a 50-observation path.

rng("default")
[y,e,sp] = simulate(Mdl,50);

y, e, and sp are 50-by-1 vectors of simulated responses, innovations, and state indices, respectively.

Plot the simulated observations in separate subplots.

figure
tiledlayout(3,1)
nexttile
plot(y,"o-")
ylabel("Response")
grid on

nexttile
plot(e,"ro-")
ylabel("Innovation") 
grid on

nexttile
stairs(sp,"m",LineWidth=2)
ylabel("State Index")
yticks([1 2])

Simulate Multiple Paths

Simulate three separate, independent paths of responses, innovations, and state indices from the model. Specify a 5-period simulation horizon.

[Y,E,SP] = simulate(Mdl,5,NumPaths=3)

Y = 5×3

   -5.4315   14.1125    9.6147
   -4.1065   12.4008   11.4378
   -7.3715   13.4929   -4.1341
    1.6877   10.0315    7.0395
    2.3238   10.0453    3.3833

E = 5×3

    0.1240    4.1125   -0.3853
    1.4367    1.1670    1.5534
   -1.9609    1.9502   -0.2779
   -0.2796   -1.4965    0.9921
   -1.7082   -0.6627   -2.9017

SP = 5×3

     2     1     1
     2     1     1
     2     1     2
     1     1     1
     1     1     1

Mdl.StateNames(SP(2,1))

ans = 
"Recession"

Y, E, and SP are 5-by-3 matrices of simulated responses, innovations, and state indices, respectively.

• The simulated response in the second period of the first path is –4.1065.

• The corresponding simulated innovation in the second period of the first path is 1.4367.

• The corresponding simulated state of the economy in the second period of the first path is a recession.

Simulate Model Containing Regression Component

Include a known regression component in each submodel. During an expansion, the ARX(2) submodel is:

$$y_t=5+0.3y_{t-1}+0.2y_{t-2}+2x_t+{\epsilon }_{1t}.$$

During a recession, the ARX(1) submodel is:

$$y_t=-5+0.1y_{t-1}+x_t+{\epsilon }_{2t}.$$

Specify the regression coefficient values of each submodel by setting the Beta property using dot notation. Then, create a new Markov-switching model from the modified ARX submodels and the existing Markov chain mc.

mdl1.Beta = 2;
mdl2.Beta = 1;
Mdl = msVAR(mc,[mdl1; mdl2]);

simulate requires exogenous data over the simulation horizon for the regression component. Generate a 50-by-1 matrix of iid standard normal observations for the required exogenous data.

x = randn(50,1);

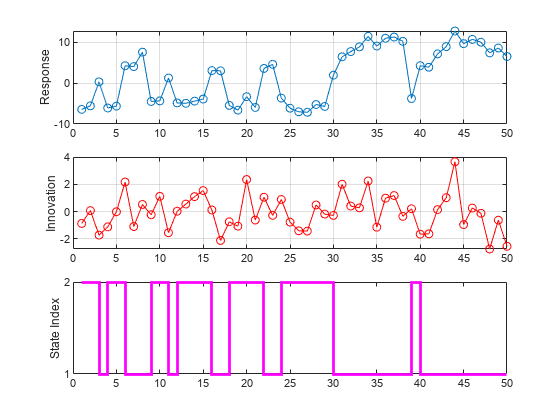
Simulate one path of responses, innovations, and state indices from the model. Specify a 50-period simulation horizon. Plot the results.

[y,e,sp] = simulate(Mdl,50,X=x);

figure
tiledlayout(3,1)
nexttile
plot(y,"o-")
ylabel("Response")
grid on

nexttile
plot(e,"ro-")
ylabel("Innovation") 
grid on

nexttile
stairs(sp,"m",LineWidth=2)
ylabel("State Index")
yticks([1 2])