Minimizing Lowpass FIR Filter Length
This example shows how to minimize the number coefficients, by designing minimum-phase or minimum-order filters.
Minimum-Phase Lowpass Filter Design
To start, set up the filter parameters and use fdesign to create a constructor for designing the filter.
N = 100;
Fp = 0.38;
Fst = 0.42;
Ap = 0.06;
Ast = 60;
Hf = fdesign.lowpass('Fp,Fst,Ap,Ast',Fp,Fst,Ap,Ast);So far, we have only considered linear-phase designs. Linear phase is desirable in many applications. Nevertheless, if linear phase is not a requirement, minimum-phase designs can provide significant improvements over linear phase counterparts. For instance, returning to the minimum order case, a minimum-phase/minimum-order design for the same specifications can be computed with:
Hd1 = design(Hf,'equiripple',SystemObject=true); Hd2 = design(Hf,'equiripple',minphase=true,... SystemObject=true); filterAnalyzer(Hd1,Hd2,... FilterNames=["LinearPhaseEquirippleDesign",... "MinimumPhaseEquirippleDesign"]);
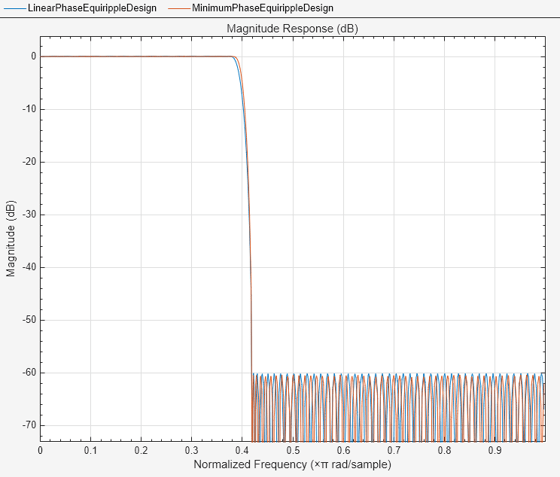
Notice that the number of coefficients has been reduced from 146 to 117. As a second example, consider the design with a stopband decaying in linear fashion. Notice the increased stopband attenuation. The passband ripple is also significantly smaller.
setspecs(Hf,'N,Fp,Fst',N,Fp,Fst); Hd3 = design(Hf,'equiripple',StopbandShape='linear',... StopbandDecay=53.333,SystemObject=true); setspecs(Hf,'Fp,Fst,Ap,Ast',Fp,Fst,Ap,Ast); Hd4 = design(Hf,'equiripple',StopbandShape='linear',... StopbandDecay=53.333,minphase=true,SystemObject=true); filterAnalyzer(Hd3,Hd4,... FilterNames=["LinearPhaseEquiDesignLinearlyDecayingStopband",... "MinimumPhaseEquiDesignLinearlyDecayingStopband"]);

Minimum-Order Lowpass Filter Design Using Multistage Techniques
A different approach to minimizing the number of coefficients that does not involve minimum-phase designs is to use multistage techniques. Here we show an interpolated FIR (IFIR) approach. The number of nonzero coefficients required in the IFIR case is 111. Less than both the equiripple linear-phase and minimum-phase designs.
Hd5 = ifir(Hf,SystemObject=true); filterAnalyzer(Hd1,Hd5,... FilterNames=["LinearPhaseEquirippleDesign",... "LinearPhaseIFIRDesign"]);
