dsp.IIRFilter
Infinite impulse response (IIR) filter
Description
The dsp.IIRFilter
System object™ filters each channel of the input using the specified filter. You can specify
the filter to have a 'Direct form I', 'Direct form I
transposed', 'Direct form II', or a 'Direct form II
transposed' structure.
Use the Numerator and Denominator properties to specify the coefficients of the filter
numerator and denominator coefficients. In addition to these coefficients, you can also
specify nonzero initial filter states through the InitialConditions
property.
To filter a signal using an IIR filter:
Create the
dsp.IIRFilterobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
iir = dsp.IIRFilter
iir = dsp.IIRFilter(num,den)Numerator property to
num and the Denominator property to
den. (since R2024a)
iir = dsp.IIRFilter(Name=Value)
Example: iir = dsp.IIRFilter(Structure='Direct form I') creates a
dsp.IIRFilter object with the Structure property
set to 'Direct form I'.
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
IIR filter structure, specified as 'Direct form I',
'Direct form I transposed', 'Direct form II', or
'Direct form II transposed'.
Numerator coefficients, specified as a row vector.
Example: [0.0296 0.1775 0.4438 0.5918 0.4438 0.1775
0.0296]
Tunable: Yes
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Complex Number Support: Yes
Denominator coefficients, specified as a row vector. The leading denominator
coefficient must equal 1.
Example: [1.0000 -0.0000 0.7777 -0.0000 0.1142 -0.0000
0.0018]
Tunable: Yes
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Complex Number Support: Yes
Initial conditions of the filter states, specified as one of the following:
scalar –– The object initializes all delay elements in the filter to the scalar value.
vector –– The length of the vector equals the number of delay elements in the filter. Each vector element specifies a unique initial condition for the corresponding delay element. The object applies the same vector to each channel of the input signal.
matrix –– The number of rows in the matrix must equal the number of delay elements in the filter. The number of columns in the matrix must equal the number of channels in the input. Each element specifies a unique initial condition for the corresponding delay element in the corresponding channel.
The number of filter states equals max(N,M) – 1, where N is the number of poles, and M is the number of zeros.
Tunable: Yes
Dependencies
This property applies only when you set the Structure property to 'Direct form
II' or 'Direct form II transposed'.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Complex Number Support: Yes
Initial conditions of the filter states on the side of the filter structure with the zeros, specified as one of the following:
scalar –– The object initializes all delay elements on the zeros side in the filter to the scalar value.
vector –– The length of the vector equals the number of delay elements on the zeros side in the filter. Each vector element specifies a unique initial condition for the corresponding delay element on the zeros side. The object applies the same vector of initial conditions to each channel of the input signal.
matrix –– The number of rows in the matrix must equal the number of delay elements on the zeros side in the filter. The number of columns in the matrix must equal the number of channels in the input signal. Each element specifies a unique initial condition for the corresponding delay element on the zeros side in the corresponding channel.
The number of filter states equals max(N,M) – 1, where N is the number of poles, and M is the number of zeros, respectively.
Tunable: Yes
Dependencies
This property applies only when you set the Structure property to 'Direct form
I' or 'Direct form I transposed'.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Complex Number Support: Yes
Initial conditions of the filter states on the side of the filter structure with the poles, specified as one of the following:
scalar –– The object initializes all delay elements on the poles side in the filter to the scalar value.
vector –– The length of the vector equals the number of delay elements on the poles side in the filter. Each vector element specifies a unique initial condition for the corresponding delay element on the poles side. The object applies the same vector of initial conditions to each channel of the input signal.
matrix –– The number of rows in the matrix must equal the number of delay elements on the poles side in the filter. The number of columns in the matrix must equal the number of channels in the input signal. Each element specifies a unique initial condition for the corresponding delay element on the poles side in the corresponding channel.
The number of filter states equals max(N,M) – 1, where N is the number of poles, and M is the number of zeros, respectively.
Tunable: Yes
Dependencies
This property applies only when you set the Structure property to 'Direct form
I' or 'Direct form I transposed'.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Complex Number Support: Yes
Fixed-Point Properties
Select the rounding mode for fixed-point operations.
Overflow action for fixed-point operations, specified as one of the following:
'Wrap'–– The object wraps the result of its fixed-point operations.'Saturate'–– The object saturates the result of its fixed-point operations.
For more details on overflow actions, see overflow mode for fixed-point operations.
State data type, specified as one of the following:
'Same as input'–– The state data type is same as the input data type.'Custom'–– The state output data type is an autosigned numeric type through the CustomStateDataType property.
State word and fraction lengths, specified as an autosigned numeric type with a word length of 16 and a fraction length of 15.
Dependencies
This property applies only when you set StateDataType to
'Custom'.
Data type of numerator coefficients, specified as one of the following:
'Same word length as input'–– The word length of the numerator coefficients is the same as the input word length. The fraction length is chosen to give the best possible precision.'Custom'–– The data type of the numerator coefficients is the autosigned numeric type specified by the CustomNumeratorCoefficientsDataType property.
Word and fraction lengths of the numerator coefficients, specified as an autosigned numeric type with a word length of 16 and a fraction length of 15.
Dependencies
This property applies only when you set NumeratorCoefficientsDataType to
'Custom'.
Data type of the denominator coefficients, specified as one of the following:
'Same word length as input'–– The word length of the denominator coefficients is the same as that of the input word length. The fraction length is chosen to give the best possible precision.'Custom'–– The data type of the denominator coefficients is the autosigned numeric type specified by the CustomDenominatorCoefficientsDataType property.
Word and fraction lengths of denominator coefficients, specified as an autosigned numeric type with a word length of 16 and a fraction length of 15.
Dependencies
This property applies only when you set DenominatorCoefficientsDataType to
'Custom'.
Data type of the output of a product operation in the numerator polynomial of the IIR filter, specified as one of the following:
'Full precision'–– The object computes the numerator product output data type using the full-precision rules. These rules provide the most accurate fixed-point numerics. No quantization occurs. Bits are added, as needed, to ensure that no roundoff or overflow occurs.'Same as input'–– The product output data type is the same as the input data type.'Custom'–– The product output data type is the custom numeric type specified by the CustomNumeratorProductDataType property. The rounding method and the overflow action are specified by the RoundingMethod and OverflowAction properties.
Numerator product word and fraction lengths, specified as an autosigned numeric type with a word length of 32 and a fraction length of 30.
Dependencies
This property applies only when you set NumeratorProductDataType to
'Custom'.
Data type of the output of a product operation in the denominator polynomial of the IIR filter, specified as one of the following:
'Full precision'–– The object computes the denominator product output data type using the full-precision rules. These rules provide the most accurate fixed-point numerics. No quantization occurs. Bits are added, as needed, to ensure that no roundoff or overflow occurs.'Same as input'–– The product output data type is the same as the input data type.'Custom'–– The product output data type is custom numeric type specified by the CustomDenominatorProductDataType property. The rounding method and the overflow action are specified by the RoundingMethod and OverflowAction properties.
Denominator product word and fraction lengths, specified as an autosigned numeric type with a word length of 32 and a fraction length of 30.
Dependencies
This property applies only when you set DenominatorProductDataType to
'Custom'.
Data type of the output of an accumulation operation in the numerator polynomial of the IIR filter, specified as one of the following:
'Full precision'–– The object computes the numerator accumulator data type using the full-precision rules. These rules provide the most accurate fixed-point numerics. No quantization occurs. Bits are added, as needed, to ensure that no roundoff or overflow occurs.'Same as input'–– The accumulator data type is the same as the input data type.'Same as product'–– The accumulator data type is the same as the product output data type.'Custom'–– The accumulator data type is the custom numeric type specified by the CustomNumeratorAccumulatorDataType property. The rounding method and the overflow action are specified by the RoundingMethod and OverflowAction properties.
Numerator accumulator word and fraction lengths, specified as an autosigned numeric type with a word length of 32 and a fraction length of 30.
Dependencies
This property applies only when you set NumeratorAccumulatorDataType to
'Custom'.
Data type of the output of an accumulation operation in the denominator polynomial of the IIR filter, specified as one of the following:
'Full precision'–– The object computes the denominator accumulator data type using the full-precision rules. These rules provide the most accurate fixed-point numerics. No quantization occurs. Bits are added, as needed, to ensure that no roundoff or overflow occurs.'Same as input'–– The accumulator data type is the same as the input data type.'Same as product'–– The accumulator data type is the same as the product output data type.'Custom'–– The accumulator data type is the custom numeric type specified by the CustomDenominatorAccumulatorDataType property. The rounding method and the overflow action are specified by the RoundingMethod and OverflowAction properties.
Denominator accumulator word and fraction lengths, specified as an autosigned numeric type with a word length of 32 and a fraction length of 30.
Dependencies
This property applies only when you set DenominatorAccumulatorDataType to
'Custom'.
Data type of the output of the dsp.IIRFilter object, specified as
one of the following:
'Same as input'–– The output data type is the same as the input data type.'Full precision'–– The object computes the output data type using the full-precision rules. These rules provide the most accurate fixed-point numerics. No quantization occurs. Bits are added, as needed, to ensure that no roundoff or overflow occurs.'Custom'–– The output data type is the custom numeric type specified by the CustomOutputDataType property. The rounding method and the overflow action are specified by the RoundingMethod and OverflowAction properties.
Output word and fraction lengths, specified as an autosigned numeric type with a word length of 16 and a fraction length of 15.
Dependencies
This property applies only when you set OutputDataType to
'Custom'.
Multiplicand data type, specified as one of the following:
'Same as input'–– The multiplicand data type is the same as the input data type.'Custom'–– The multiplicand data type is the autosigned numeric type specifies by the CustomMultiplicandDataType property.
Multiplicand output word and fraction lengths, specified as an autosigned numeric type with a word length of 16 and a fraction length of 15.
Dependencies
This property applies only when you set MultiplicandDataType to
'Custom'.
Usage
Syntax
Description
Input Arguments
Data input that is filtered, specified as a vector or matrix.
The input data can be a variable-size signal, that is, the frame length (number of rows) of the signal can change during simulation but the number of channels (columns) must remain constant. (since R2024a)
Data Types: single | double | int8 | int16 | int32 | int64 | fi
Complex Number Support: Yes
Output Arguments
Filtered output, returned as a vector or a matrix. The size, data type, and complexity of the output match that of the input.
Data Types: single | double | int8 | int16 | int32 | int64 | fi
Complex Number Support: Yes
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
freqz | Frequency response of discrete-time filter System object |
filterAnalyzer | Analyze filters with Filter Analyzer app |
impz | Impulse response of discrete-time filter System object |
phasez | Phase response of discrete-time filter System object (unwrapped) |
sos | Convert to second order sections |
outputDelay | Determine output delay of single-rate or multirate filter |
For a list of filter analysis methods this object supports, type
dsp.IIRFilter.helpFilterAnalysis in the MATLAB® command prompt. For the corresponding function reference pages, see Analysis Functions for Filter System Objects.
Examples
Filter a noisy sinusoidal signal using a lowpass Butterworth IIR filter.
Input Signal
The input signal has three tones, 1 kHz, 5 kHz, and 12 kHz.
Sine1 = dsp.SineWave(Frequency=1e3,... SampleRate=44.1e3); Sine2 = dsp.SineWave(Frequency=5e3,... SampleRate=44.1e3); Sine3 = dsp.SineWave(Frequency=12e3,... SampleRate=44.1e3);
Filter Design
Use the butter function to design a 10th order lowpass Butterworth filter.
N = 10; Fc = 0.4; [b,a] = butter(N,Fc);
Create a dsp.IIRFilter object and assign the designed coefficients to the Numerator and the Denominator properties.
iir = dsp.IIRFilter(b,a)
iir =
dsp.IIRFilter with properties:
Structure: 'Direct form II transposed'
Numerator: [4.9945e-04 0.0050 0.0225 0.0599 0.1049 0.1259 0.1049 0.0599 0.0225 0.0050 4.9945e-04]
Denominator: [1 -1.9924 3.0195 -2.8185 2.0387 -1.0545 0.4144 -0.1157 0.0225 -0.0027 1.4876e-04]
InitialConditions: 0
Show all properties
View the magnitude response of the filter. The cutoff frequency is at 0.4 rad/sample, which, with a sample rate of 44.1 kHz, translates to or 8.82 kHz.
filterAnalyzer(iir,SampleRates=Sine1.SampleRate)

View the power spectrum of the input and output signal using the Spectrum Analyzer.
sa = spectrumAnalyzer(SampleRate=Sine1.SampleRate,... Method='welch',... PlotAsTwoSidedSpectrum=false,... OverlapPercent=80,... SpectrumUnits='dBW',... YLimits=[-220 -10]);
Streaming
Add zero-mean white Gaussian noise with a standard deviation of 0.01 to the sum of sine waves. Filter the signal using the IIR filter.
The tones at 1 kHz and 5 kHz are unaffected since they fall in the passband. The frequency at 12 kHz is attenuated since it falls in the transition band of the filter.
for i = 1:5000 input = Sine1()+Sine2()+Sine3()+... 0.01*randn(Sine1.SamplesPerFrame,1); output = iir(input); sa(input,output) end

Design a notching comb filter with 8 notches, and a notch bandwidth of 0.02 referenced to a -3 dB level.
Create a comb filter design specification object using the fdesign.comb function and specify these design parameters.
combSpecs = fdesign.comb('notch','N,BW',8,0.02);
Design the notching comb filter using the design function. The resulting filter is a dsp.IIRFilter System object™. For details on how to apply this filter on streaming data, refer to dsp.IIRFilter.
iirFilt = design(combSpecs,Systemobject=true)
iirFilt =
dsp.IIRFilter with properties:
Structure: 'Direct form II'
Numerator: [0.8878 0 0 0 0 0 0 0 -0.8878]
Denominator: [1 0 0 0 0 0 0 0 -0.7757]
InitialConditions: 0
Show all properties
View magnitude response of the designed filter.
filterAnalyzer(iirFilt)

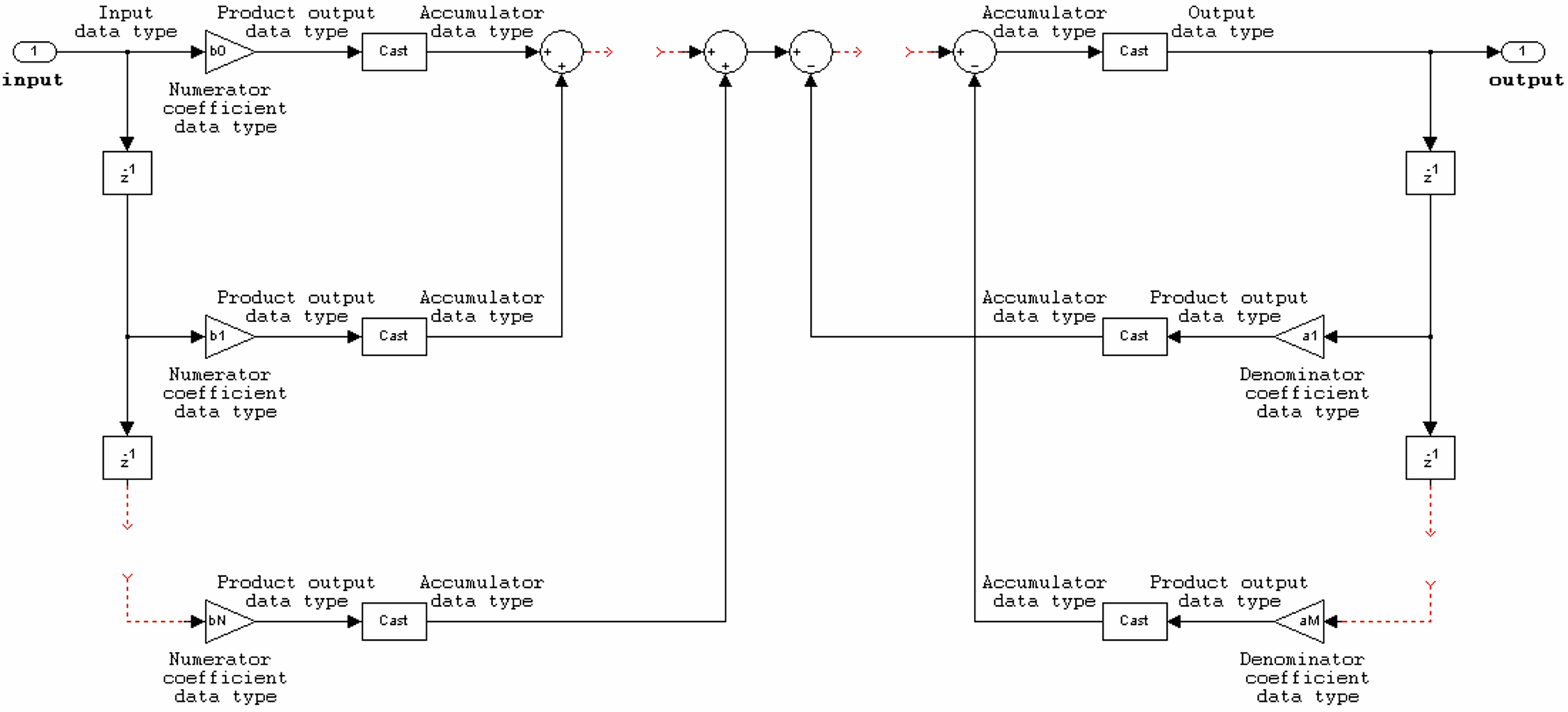
More About
The dsp.IIRFilter
System object supports the following filter structures. The diagrams in each section show
the data types used in the filter structures for fixed-point signals. You can set the data
types using the fixed-point properties of the object.

The following constraints apply when the Structure property is
set to 'Direct form I':
Inputs can be real or complex.
Numerator and denominator coefficients can be real or complex.
Numerator and denominator coefficients must have the same complexity characteristics. When the numerator and denominator coefficients have different complexities from each other, the object processes the filter as if two sets of complex coefficients are provided. The real-valued coefficient set is treated as if it is a complex vector with zero-valued imaginary parts.
The State data type cannot be specified for this structure. Doing so is not possible because the input and output states have the same data types as the input and output buffers.

The following constraints apply when the Structure property is
set to 'Direct form I transposed':
Inputs can be real or complex.
Numerator and denominator coefficients can be real or complex.
Numerator and denominator coefficients must have the same complexity characteristics. When the numerator and denominator coefficients have different complexities from each other, the object processes the filter as if two sets of complex coefficients are provided. The real-valued coefficient set is treated as if it is a complex vector with zero-valued imaginary parts.
States are complex when either the input or the coefficients are complex.


The following constraints apply when the Structure property is
set to 'Direct form II':
Inputs can be real or complex.
Numerator and denominator coefficients can be real or complex.
Numerator and denominator coefficients must have the same complexity characteristics. When the numerator and denominator coefficients have different complexities from each other, the object processes the filter as if two sets of complex coefficients are provided. The real-valued coefficient set is treated as if it is a complex vector with zero-valued imaginary parts.
States are complex when either the inputs or the coefficients are complex.


The following constraints apply when the Structure property is
set to 'Direct form II transposed':
Inputs can be real or complex.
Numerator and denominator coefficients can be real or complex.
Numerator and denominator coefficients must have the same complexity characteristics. When the numerator and denominator coefficients have different complexities from each other, the object processes the filter as if two sets of complex coefficients are provided. The real-valued coefficient set is treated as if it is a complex vector with zero-valued imaginary parts.
States are complex when either the inputs or the coefficients are complex.

Extended Capabilities
Usage notes and limitations:
Only the
NumeratorandDenominatorproperties are tunable for code generation.See System Objects in MATLAB Code Generation (MATLAB Coder).
Version History
Introduced in R2012bYou can now specify the Numerator and
Denominator property values as value-only arguments while
constructing the dsp.IIRFilter object.
iir = dsp.IIRFilter(1:3,[1,1/2,1/3])
iir =
dsp.IIRFilter with properties:
Structure: 'Direct form II transposed'
Numerator: [1 2 3]
Denominator: [1 0.5000 0.3333]
InitialConditions: 0
Show all properties
You can now input variable-size signals to the dsp.IIRFilter object.
The signal frame size can change during simulation but the number of channels must remain
constant.
iir = dsp.IIRFilter(1:3,[1,1/2,1/3])
iir =
dsp.IIRFilter with properties:
Structure: 'Direct form II transposed'
Numerator: [1 2 3]
Denominator: [1 0.5000 0.3333]
InitialConditions: 0
Show all properties
You can also change the frame size while the object is locked.
y = iir(randn(14,1)); y = iir(randn(24,1));
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)