interpolate
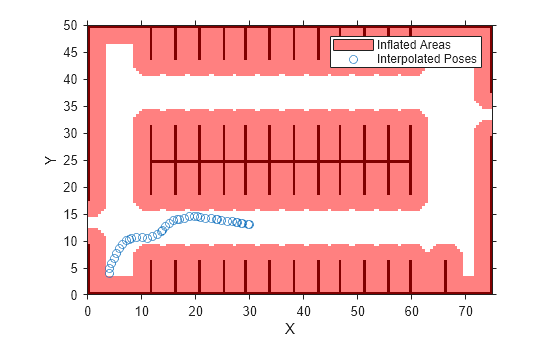
Interpolate poses along planned vehicle path
Syntax
Description
poses = interpolate(refPath)
[
also returns the motion directions of the vehicle at each pose, using inputs from any of the
preceding syntaxes.poses,directions] = interpolate(___)
Examples
Input Arguments
Output Arguments
More About
Extended Capabilities
Version History
Introduced in R2018b