lqg
Linear-Quadratic-Gaussian (LQG) design
Syntax
reg = lqg(sys,QXU,QWV)
reg = lqg(sys,QXU,QWV,QI)
reg = lqg(sys,QXU,QWV,QI,'1dof')
reg = lqg(sys,QXU,QWV,QI,'2dof')
reg = lqg(___,'current')
[reg,info] = lqg(___)
Description
reg = lqg(sys,QXU,QWV) computes an optimal
linear-quadratic-Gaussian (LQG) regulator reg given
a state-space model sys of the plant and weighting
matrices QXU and QWV. The dynamic
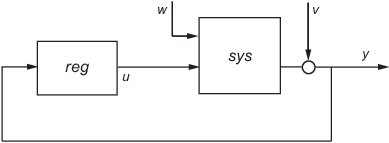
regulator reg uses the measurements y to
generate a control signal u that regulates y around
the zero value. Use positive feedback to connect this regulator to
the plant output y.
The LQG regulator minimizes the cost function
subject to the plant equations
where the process noise w and measurement noise v are Gaussian white noises with covariance:
reg = lqg(sys,QXU,QWV,QI) uses the setpoint
command r and measurements y to
generate the control signal u. reg has
integral action to ensure that y tracks the command r.

The LQG servo-controller minimizes the cost function
where xi is the integral of the tracking error r - y. For MIMO systems, r, y, and xi must have the same length.
reg = lqg(sys,QXU,QWV,QI,'1dof') computes
a one-degree-of-freedom servo controller that takes e = r - y rather
than [r ; y] as input.
reg = lqg(sys,QXU,QWV,QI,'2dof') is equivalent
to LQG(sys,QXU,QWV,QI) and produces the two-degree-of-freedom
servo-controller shown previously.
reg = lqg(___,'current') uses the "current" Kalman estimator, which
uses x[n|n] as the state estimate
when computing an LQG regulator for a discrete-time system.
[reg,info] = lqg(___) returns the controller and estimator gain
matrices in the structure info for any of the previous syntaxes. You can
use the controller and estimator gains to, for example, implement the controller in observer
form. For more information, see Algorithms.
Examples
Linear-Quadratic-Gaussian (LQG) Regulator and Servo Controller Design
This example shows how to design an linear-quadratic-Gaussian (LQG) regulator, a one-degree-of-freedom LQG servo controller, and a two-degree-of-freedom LQG servo controller for the following system.
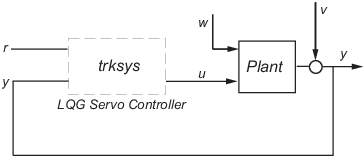
The plant has three states (x), two control inputs (u), three random inputs (w), one output (y), measurement noise for the output (v), and the following state and measurement equations.
where
The system has the following noise covariance data:
For the regulator, use the following cost function to define the tradeoff between regulation performance and control effort:
For the servo controllers, use the following cost function to define the tradeoff between tracker performance and control effort:
To design the LQG controllers for this system:
Create the state-space system by typing the following in the MATLAB Command Window:
A = [0 1 0;0 0 1;1 0 0]; B = [0.3 1;0 1;-0.3 0.9]; C = [1.9 1.3 1]; D = [0.53 -0.61]; sys = ss(A,B,C,D);
Define the noise covariance data and the weighting matrices by typing the following commands:
nx = 3; %Number of states ny = 1; %Number of outputs Qn = [4 2 0; 2 1 0; 0 0 1]; Rn = 0.7; R = [1 0;0 2] QXU = blkdiag(0.1*eye(nx),R); QWV = blkdiag(Qn,Rn); QI = eye(ny);
Form the LQG regulator by typing the following command:
This command returns the following LQG regulator:KLQG = lqg(sys,QXU,QWV)
A = x1_e x2_e x3_e x1_e -6.212 -3.814 -4.136 x2_e -4.038 -3.196 -1.791 x3_e -1.418 -1.973 -1.766 B = y1 x1_e 2.365 x2_e 1.432 x3_e 0.7684 C = x1_e x2_e x3_e u1 -0.02904 0.0008272 0.0303 u2 -0.7147 -0.7115 -0.7132 D = y1 u1 0 u2 0 Input groups: Name Channels Measurement 1 Output groups: Name Channels Controls 1,2 Continuous-time model.Form the one-degree-of-freedom LQG servo controller by typing the following command:
This command returns the following LQG servo controller:KLQG1 = lqg(sys,QXU,QWV,QI,'1dof')A = x1_e x2_e x3_e xi1 x1_e -7.626 -5.068 -4.891 0.9018 x2_e -5.108 -4.146 -2.362 0.6762 x3_e -2.121 -2.604 -2.141 0.4088 xi1 0 0 0 0 B = e1 x1_e -2.365 x2_e -1.432 x3_e -0.7684 xi1 1 C = x1_e x2_e x3_e xi1 u1 -0.5388 -0.4173 -0.2481 0.5578 u2 -1.492 -1.388 -1.131 0.5869 D = e1 u1 0 u2 0 Input groups: Name Channels Error 1 Output groups: Name Channels Controls 1,2 Continuous-time model.Form the two-degree-of-freedom LQG servo controller by typing the following command:
This command returns the following LQG servo controller:KLQG2 = lqg(sys,QXU,QWV,QI,'2dof')A = x1_e x2_e x3_e xi1 x1_e -7.626 -5.068 -4.891 0.9018 x2_e -5.108 -4.146 -2.362 0.6762 x3_e -2.121 -2.604 -2.141 0.4088 xi1 0 0 0 0 B = r1 y1 x1_e 0 2.365 x2_e 0 1.432 x3_e 0 0.7684 xi1 1 -1 C = x1_e x2_e x3_e xi1 u1 -0.5388 -0.4173 -0.2481 0.5578 u2 -1.492 -1.388 -1.131 0.5869 D = r1 y1 u1 0 0 u2 0 0 Input groups: Name Channels Setpoint 1 Measurement 2 Output groups: Name Channels Controls 1,2 Continuous-time model.
Tips
lqgcan be used for both continuous- and discrete-time plants. In discrete time,lqguses x[n|n-1] as its state estimate by default. To use x[n|n] as the state estimate and compute the optimal LQG controller, use the'current'input argument. For details on the state estimators, seekalman.To compute the LQG regulator,
lqguses the commandslqrandkalman. To compute the servo-controller,lqguses the commandslqiandkalman.When you want more flexibility for designing regulators, you can use the
lqr,kalman, andlqgregcommands. When you want more flexibility for designing servo controllers, you can use thelqi,kalman, andlqgtrackcommands. For more information on using these commands and how to decide when to use them, see Linear-Quadratic-Gaussian (LQG) Design for Regulation and Linear-Quadratic-Gaussian (LQG) Design of Servo Controller with Integral Action.
Algorithms
The controller equations are:
For continuous time:
For discrete time:
Delayed estimator:
Current estimator:
Here,
A, B, C, and D are the state-space matrices of the LQG regulator,
reg.xi is the integral of the tracking error r - y.
Kx, Kw, Ki, L, Mx, and Mw are the controller and estimator gain matrices returned in
info.
Version History
Introduced before R2006a