inv
Invert dynamic system models
Syntax
inv
inv(sys,'min')
Description
inv inverts the input/output
relation
to produce the model with the transfer matrix .
This operation is defined only for square systems (same number of inputs and
outputs) with an invertible feedthrough matrix D.
inv handles both continuous- and discrete-time
systems.
inv(sys,'min') inverts sys to eliminate
the extra states and obtain a model with as many states as sys
or A respectively. For ss,
genss and uss models, the inverse
model is returned in implicit form by default. This option is ignored for sparse
models because it typically destroys sparsity. Use isproper or
ss(sys,'explicit') to extract an explicit model if
desired.
Examples
Consider
At the MATLAB® prompt, type
H = [1 tf(1,[1 1]);0 1] Hi = inv(H)
to invert it. These commands produce the following result.
Transfer function from input 1 to output...
#1: 1
#2: 0
Transfer function from input 2 to output...
-1
#1: -----
s + 1
#2: 1
You can verify that
H * Hi
is the identity transfer function (static gain I).
Limitations
Do not use inv to model feedback connections such as
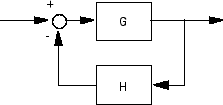
While it seems reasonable to evaluate the corresponding closed-loop transfer function as
inv(1+g*h) * g
this typically leads to nonminimal closed-loop models. For example,
g = zpk([],1,1) h = tf([2 1],[1 0]) cloop = inv(1+g*h) * g
yields a third-order closed-loop model with an unstable pole-zero cancellation at
s = 1.
cloop
Zero/pole/gain:
s (s-1)
-------------------
(s-1) (s^2 + s + 1)
Use feedback to avoid such pitfalls.
cloop = feedback(g,h)
Zero/pole/gain:
s
-------------
(s^2 + s + 1)
Version History
Introduced before R2006a