Idealized Baseband Amplifier with Nonlinearity and Noise
The example shows how to use the idealized baseband library Amplifier block to amplify a signal with nonlinearity and noise. The Amplifier uses the Cubic Polynomial model with a Linear power gain of 10 dB, an Input IP3 nonlinearity of 30 dBm, and a Noise figure of 3 dB.

System Architecture
The DSP Sine Wave block inputs two complex baseband tones with a power level of -20 dBm and -25 dBm at frequencies of -30 MHz and 20 MHz. In this block you can also:
Increase the samples per frame to increase the simulation speed.
Use output complexity and phase offset to control the I-Q relationship of each baseband signal
Control the bandwidth of the scopes using the inverse of the sample time parameter.
The Amplifier block only accepts a vector input. The Sum block combines the two baseband signals into a vector length equal to the samples per frame in the DSP Sine Wave block.
The Thermal Noise block creates a thermal noise floor input of -174 dBm/Hz.
Simulation Analysis
The Amplifier block with Linear power gain of 10 dB outputs tone with magnitude -10 dBm and -15 dBm as seen in the Power plot. The Amplifier also increases the thermal noise floor to -161 dBm/Hz. You can calculate the output thermal noise using:
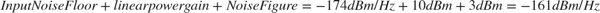
The following plots illustrate the differences in the input and output noise floors. The spurs appear at 70 MHz (2*20 MHz + 30 MHz) and -80 MHz (2*(-30 MHz) - 20 MHz). This shows the third order intercept nature of the spurs.

Increasing the Slider value from 1 to 10, shows nonlinear effects in the plots. These are the Noise and Power plots when the gain of the Slider is 10.
