Cosine Similarity As a Channel Estimate Quality Metric
Cosine similarity is a metric that measures how similar two vectors are irrespective of their size. Essentially, it calculates the cosine of the angle between two vectors in a multidimensional space, ranging from –1 (exactly opposite) to 1 (exactly the same), with 0 indicating orthogonality. This metric is particularly useful when the magnitude of the vectors is less important than the direction they point. When the vectors contain complex numbers, cosine similarity still aims to quantify how similar two vectors are in terms of their direction, but it incorporates the phase information inherent in complex numbers. The magnitude of the complex similarity metric shows how similar the vectors are while the angle of the metric relates to the phase difference between the vectors. This phase information is essential for applications in fields like wireless communication and signal processing.
For 5G systems and beyond, using neural networks to compress channel state information (CSI) is key for sending data efficiently. These neural networks seek to reduce the amount of resources required to feedback CSI over the network. The goal is to compress and send CSI that keeps all the important details intact, and to preserve the quality and usefulness of the CSI.
Cosine similarity becomes very important in neural networks that compress the CSI because it serves as a metric to quantify the quality of the neural network that compresses and then decompresses the CSI. Cosine similarity compares the original CSI with the decompressed version to quantify how closely they match. A high score means the decompressed data is very similar to the original, indicating that the compression process worked well without losing important information. This feedback is crucial for fine-tuning the neural network, making sure that the compressed CSI data retains details required for accurate network decisions, such as adjusting signals for low-error rate communications. Ultimately, this metric leads to more efficient use of network resources and better network performance.
Generic Cosine Similarity for Matrices
Given an -by- data matrix , which is treated as (1-by-) row vectors , , ..., , and an -by- data matrix , which is treated as (1-by-) row vectors , , ..., , the cosine similarity between the vector and are defined as follows:
.
The helperComplexCosineSimilarity function calculates the cosine similarity between the row of and row of . Create the matrix as a random complex-valued matrix.
rng(123) % Generate same numbers X = randn(4,3,"like",1i)
X = 4×3 complex
0.5404 - 0.4278i -0.0233 - 0.2087i -0.6441 - 0.3274i
-0.7318 + 0.1424i -0.3923 + 0.3991i 0.0868 + 0.0637i
0.4723 - 0.2287i -0.0946 - 1.1849i 0.2262 + 0.7520i
0.9435 + 0.4394i -0.2465 + 0.5979i 0.6372 + 0.2031i
The matrix is the noisy version of .
Y = awgn(X,10)
Y = 4×3 complex
0.6792 - 0.5721i -0.0525 - 0.2112i -0.5521 - 0.5331i
-0.8135 + 0.0120i -0.4151 + 0.1926i -0.0387 - 0.0079i
0.1660 - 0.1073i -0.1616 - 0.8501i 0.6504 + 0.6647i
0.5617 + 0.4250i 0.0638 + 0.5991i 0.6256 + 0.4346i
The helperComplexCosineSimilarity function calculates the cosine similarity between rows of two arrays. When the operation method is "perm", the function calculates the similarity for all permutations of rows. Since is the noisy version of , the diagonal similarity values are close to 1. Since the rows of X are independent, the off-diagonal values are smaller.
cosimperm = helperComplexCosineSimilarity(X,Y,"perm")cosimperm = 4×4 complex
0.9747 + 0.1133i -0.6464 + 0.3702i 0.0999 + 0.0759i -0.1104 - 0.5895i
-0.4697 - 0.4618i 0.9500 + 0.2270i -0.4164 - 0.4676i -0.4378 + 0.4388i
-0.2438 - 0.1647i -0.2602 + 0.3889i 0.9081 - 0.2370i 0.1061 + 0.2359i
-0.4492 + 0.3220i -0.0484 - 0.5806i -0.0437 - 0.0132i 0.9231 + 0.0705i
Cosine Similarity for CSI
When is a channel matrix, only the similarity between the row of and row are important. Call the helperComplexCosineSimilarity function with the "rows" option.
cosimrows = helperComplexCosineSimilarity(X,Y,"rows")cosimrows = 4×1 complex
0.9747 + 0.1133i
0.9500 + 0.2270i
0.9081 - 0.2370i
0.9231 + 0.0705i
Calling the function with the "meanrows" option calculates the mean of cosine similarity of all the corresponding rows, which is calculated using the "rows" option. The "meanrows" operation method is the default value.
cosimmean = helperComplexCosineSimilarity(X,Y)
cosimmean = 0.9390 + 0.0434i
Test With Compressed and Decompressed CSI
Load the original channel estimate, , and the compressed and decompressed channel estimate, , obtained using 4-bit quantization in the CSI Feedback with Autoencoders example. The dimensions of are subcarriers, transmit antennas, and realizations. The and pairs have –0.78 dB, –6.4 dB, –12.5 dB NMSE for the three realizations in this example.
load csi_cosim_test_data.mat H Hhat t=tiledlayout(3,2); ylabel(t,"Subcarrier") xlabel(t,"Tx Antenna") nexttile imagesc(abs(H(:,:,1))) title("$H$",Interpreter="latex") nexttile imagesc(abs(Hhat(:,:,1))) title("$\hat{H}$",Interpreter="latex") nexttile imagesc(abs(H(:,:,2))) nexttile imagesc(abs(Hhat(:,:,2))) nexttile imagesc(abs(H(:,:,3))) nexttile imagesc(abs(Hhat(:,:,3)))
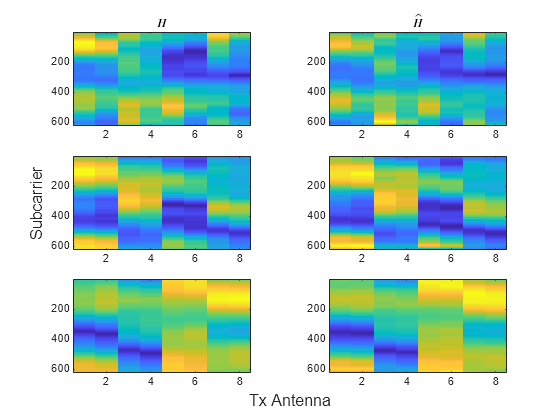
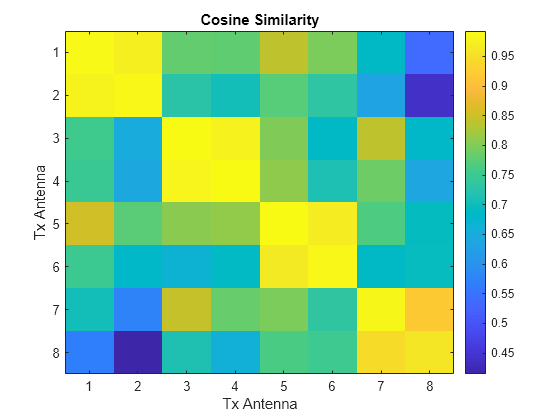
Run the cosine similarity along the subcarriers for each of the eight antennas. Since and store subcarriers in the first dimension, transpose the matrices to place subcarriers in the rows (second dimension). Off-diagonal values show the similarity between different antennas and have lower values. The helperComplexCosineSimilarity function processes all three realizations at the same time by using batch processing, where the third dimension is the batch (page) dimension. The pagectranspose function applies the complex conjugate transpose to each page of and .
cosimperm = helperComplexCosineSimilarity(pagectranspose(H),pagectranspose(Hhat),"perm");Select the index of the batch to examine.
idx =1; figure imagesc(abs(cosimperm(:,:,idx))) xlabel("Tx Antenna") ylabel("Tx Antenna") title("Cosine Similarity") colorbar
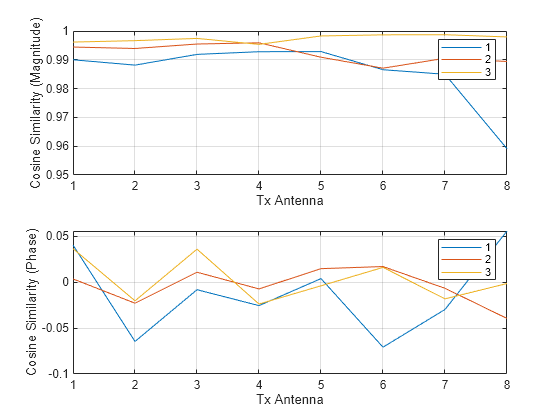
Plot the cosine similarity between the same antennas.
cosimrows = helperComplexCosineSimilarity(pagetranspose(H),pagetranspose(Hhat),"rows"); subplot(2,1,1) plot(abs(squeeze(cosimrows))) grid on xlabel("Tx Antenna") ylabel("Cosine Similarity (Magnitude)") legend("1","2","3") subplot(2,1,2) plot(angle(squeeze(cosimrows))) grid on xlabel("Tx Antenna") ylabel("Cosine Similarity (Phase)") legend("1","2","3")
Calculate cosine similarity across all Tx antennas.
cosimmean = helperComplexCosineSimilarity(pagetranspose(H),pagetranspose(Hhat))
cosimmean = cosimmean(:,:,1) = 0.9848 - 0.0123i cosimmean(:,:,2) = 0.9920 - 0.0037i cosimmean(:,:,3) = 0.9971 + 0.0026i