Expander
Dynamic range expander
Libraries:
Audio Toolbox /
Dynamic Range Control
Description
The Expander block performs dynamic range expansion independently across each input channel. Dynamic range expansion attenuates the volume of quiet sounds below a given threshold. The block uses specified attack, release, and hold times to achieve a smooth applied gain curve.
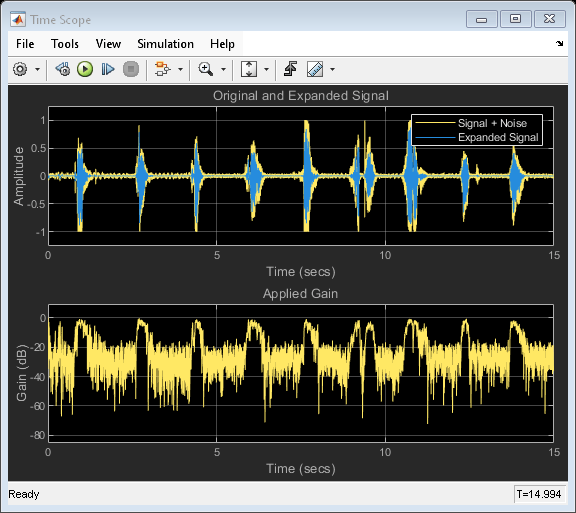
Examples
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
Algorithms
The Expander block processes a signal frame by frame and element by element.

The N-point signal, x[n], is converted to decibels:
xdB[n] passes through the gain computer. The gain computer uses the static characteristic properties of the dynamic range expander to attenuate gain that is below the threshold.
If you specified a soft knee, the gain computer has the following static characteristic:
where T is the threshold, R is the expansion ratio, and W is the knee width.
If you specified a hard knee, the gain computer has the following static characteristic:
The computed gain, gc[n], is calculated as
gc[n] is smoothed using specified attack, release, and hold time parameters:
CA is the hold counter for attack. The limit, TH, is determined by the Hold time (s) parameter.
The attack time coefficient, α A, is calculated as
The release time coefficient, α R, is calculated as
TA is the attack time period, specified by the Attack time (s) parameter. T R is the release time period, specified by the Release time (s) parameter. Fs is the input sampling rate, specified by the Inherit sample rate from input or Input sample rate (Hz) parameter.
The smoothed gain in dB, gs[n], is translated to a linear domain:
The output of the dynamic range expander is given as
References
[1] Giannoulis, Dimitrios, Michael Massberg, and Joshua D. Reiss. "Digital Dynamic Range Compressor Design –– A Tutorial And Analysis." Journal of Audio Engineering Society. Vol. 60, Issue 6, 2012, pp. 399–408.
Extended Capabilities
Version History
Introduced in R2016a