Three Ways to Estimate Remaining Useful Life for Predictive Maintenance
By Aditya Baru and Rachel Johnson, MathWorks
Remaining useful life (RUL) is the length of time a machine will operate before it requires repair or replacement. By estimating RUL, engineers can schedule maintenance, optimize operating efficiency, and avoid unplanned downtime. For this reason, estimating RUL is a top priority in predictive maintenance programs.
An RUL estimation model provides a confidence-bound RUL prediction. The model inputs are condition indicators (features) extracted from sensor data whose behavior changes in a predictable way as the system degrades.
Estimating Remaining Useful Life (RUL)
Learn about the most common RUL estimator models: similarity, survival, and degradation.
The method used to calculate RUL depends on the kind of data available:
- Lifetime data indicating how long it took for similar machines to reach failure
- Run-to-failure histories of similar machines
- A known threshold value of a condition indicator that detects failure
Predictive Maintenance Toolbox™ provides models for estimating RUL from each type of data.
Lifetime Data
Proportional hazard models and probability distributions of component failure times are used to estimate RUL from lifetime data. A simple example is estimating the discharge time of a battery based on past discharge times and covariates, such as environmental temperature and load.
The survival function plot in Figure 1 shows the probability that a battery will fail based on how long it has been in operation. The plot shows, for example, that if the battery is in operation for 75 cycles, it has a 90% chance of being at the end of its lifetime.
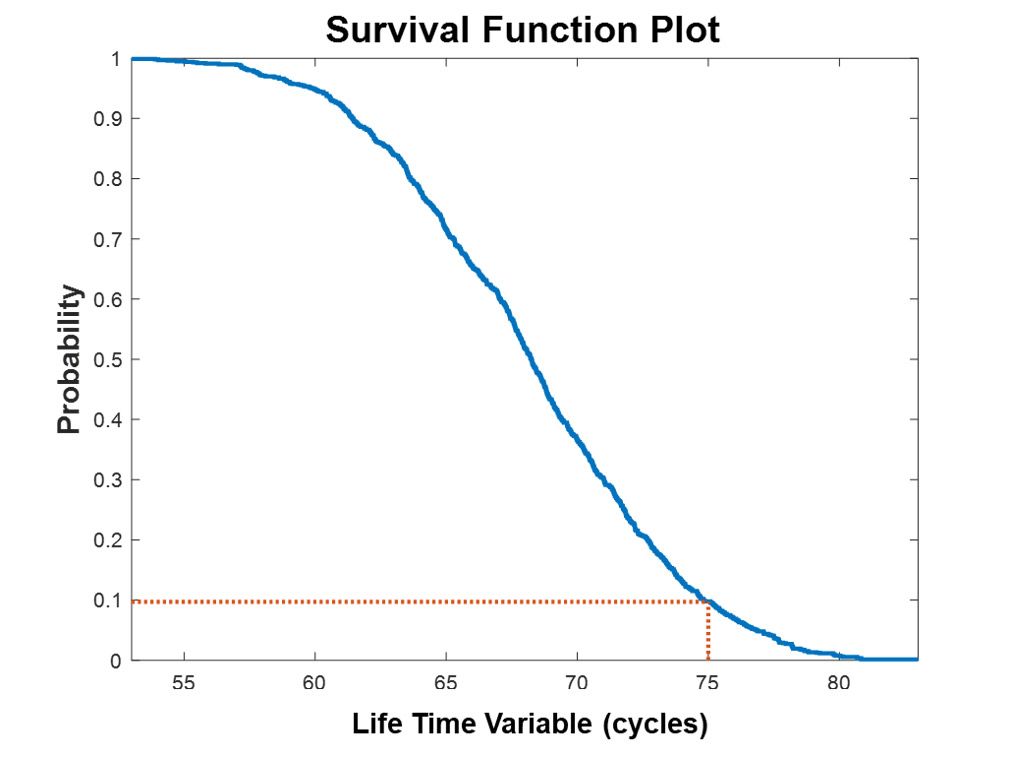
Figure 1. Survival function plot. At the end of 75 cycles, the probability of a battery continuing to operate is 0.1, or 10%. (See example)
Run-to-Failure Data
If you have a database of run-to-failure data from similar components or different components showing similar behavior, you can estimate RUL using similarity methods. These methods capture degradation profiles and compare them with new data coming in from the machine to determine which profile the data matches most closely.
In Figure 2, the degradation profiles of historical run-to-failure data sets from an engine are shown in blue and the current data from the engine is shown in red. Based on a distribution of the nearest historical profiles, the RUL is estimated to be around 65 cycles.

Figure 2. Degradation profiles (blue) based on run-to-failure data. The distribution of the stars (endpoints) of the nearest blue curves gives an RUL of 65 cycles. (See example)
Threshold Data
In many cases, a conservative maintenance schedule means machines rarely fail. This can mean run-to-failure data or lifetime data is not available. However, you likely have information on prescribed threshold values—for example, the temperature of a liquid in a pump cannot exceed 160 ˚F (71 ˚C) and the pressure must be under 2,200 psi (155 bar). With this threshold information, you can fit degradation models to condition indicators extracted from sensor data, which change linearly or exponentially over time.
These degradation models estimate RUL by predicting when the condition indicator will cross the threshold. They can also be used with a fused condition indicator that incorporates information from more than one sensor using techniques such as principal component analysis.
Figure 3 shows an exponential degradation model that tracks failure in a high-speed bearing used in a wind turbine. The condition indicator is shown in blue. The degradation model predicts that the bearing will cross the threshold value in approximately 9.5 days. The region shaded in red represents the confidence bounds for this prediction.

Figure 3. Degradation model for a high-speed bearing. The bearing has an estimated RUL of 9.5 days based on its current condition data (blue) and the exponential degradation model (red) fit to this data. (See example)
Once you have designed an RUL model based on the data you have available, you can integrate it into dashboards used by operators or alarm systems monitored by maintenance teams. Teams can then respond to changes in equipment health quickly and efficiently, and without affecting operations.
Predictive Maintenance Resources
Published 2023
