The MathWorks Logo is an Eigenfunction of the Wave Equation
By Cleve Moler, MathWorks
We hope you’ve seen it many times. It’s on the covers of our books. It’s on our business cards and stationery. It’s even on a “sponsor a highway” sign on Route 9 in Natick,Massachusetts. But, do you really know what the logo is?
I’m talking about the L-shaped membrane.We’ve used various pictures of it ever since The MathWorks was founded almost twenty years ago, but it only recently became the official company logo. I’d like to tell you about its mathematical background.
The wave equation is a fundamental model in mathematical physics that describes how a disturbance travels through matter. If t is time and x and y are spatial coordinates with the units chosen so that the wave propagation speed is equal to one, then the amplitude of a wave satisfies the partial differential equation
\[\frac{\partial^2 u}{\partial t^2} = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\]
Periodic time behavior gives solutions of the form
\[\begin{gather}u(t,x,y) = \sin\left(\sqrt{y}t\right)) v(x,y), \text{where }\\ \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} + \lambda v = 0\end{gather}\]
The quantities \(\lambda\) are the eigenvalues and the corresponding functions \(v(x,y)\) are the eigenfunctions or modes of vibration. They are determined by the physical properties, the geometry, and the boundary conditions of each particular situation. Any solution to the wave equation can be expressed as a linear combination of these eigenfunctions. The square roots of the eigenvalues are resonant frequencies. A periodic external driving force at one of these frequencies will generate an unboundedly strong response in the medium.
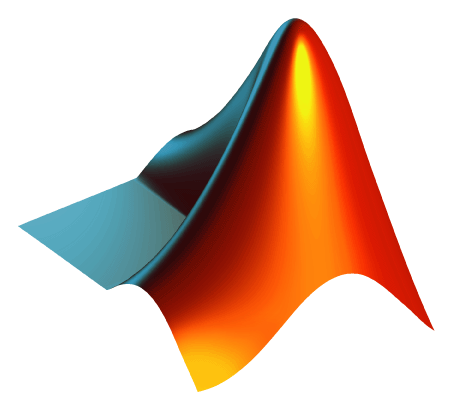
The L-shaped region formed from three unit squares is interesting for several reasons. It is one of the simplest geometries for which solutions to the wave equation cannot be expressed analytically, so numerical computation is necessary. The 270º nonconvex corner causes a singularity in the solution.Mathematically, the gradient of the first eigenfunction is unbounded near the corner. Physically, a membrane stretched over such a region would rip at the corner. This singularity limits the accuracy of finite difference methods with uniform grids.

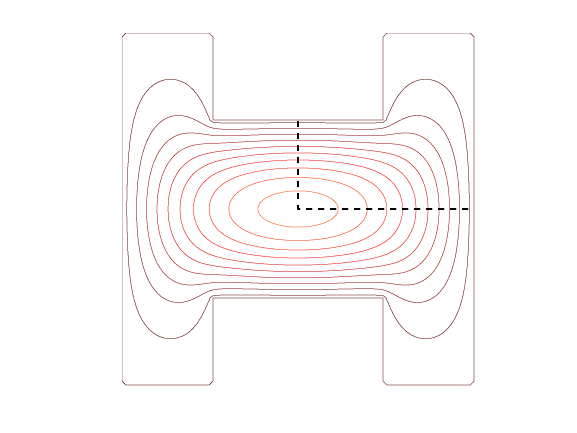
The simple physical situations involving waves on an L-shaped region include a vibrating L-shaped membrane, or tambourine, and a beach towel blowing in the wind, constrained by a picnic basket on onefourth of the towel. A more practical example involves microwave waveguides. One such device is a waveguide-to-coax adapter. The active region is the channel with the H-shaped cross section visible at the end of the adapter. The ridges increase the bandwidth of the guide at the expense of higher attenuation and lower power-handling capability. Symmetry about the dotted lines in the contour plot of the electric field in the channel implies that only one-quarter of the cross section needs to be modeled and that the resulting geometry is our L-shaped region. The boundary conditions are not the same as the membrane problem, but the differential equation and the solution techniques are the same.
You can use classic finite difference methods to compute the eigenvalues and eigenfunctions of the L-shaped membrane in MATLAB with
n = 200
h = 1/n
A = delsq(numgrid('L',2*n+1))/h^2
lambda = eigs(A,12,0)
The resulting sparse matrix A has order 119201 and 594409 nonzero entries. The eigs function uses Arnoldi’s method from the MATLAB implementation of ARPACK to compute the first 12 eigenvalues. This takes only a little over a minute on a 1.4 GHz Pentium laptop. However, the corner singularity causes the computed eigenvalues to be accurate to only three or four significant digits. If you try for more accuracy with a finer mesh and a larger matrix, you soon exceed half a gigabyte of main memory.
For the L-shaped membrane and similar problems, a technique using analytic solutions to the underlying differential equation is much more efficient and accurate than finite difference methods. The building blocks are the fractional order Bessel functions and trig functions that yield eigenfunctions of circular sectors. Remember Pac-Man? How would Pac-Man vibrate? This simple graphics character from one of the earliest video games provides a two-dimensional test domain. When he was not chomping ghosts, Pac-Man was three-quarters of the unit disc.With polar coordinates \(r\) and \(\theta\), and parameters \(\alpha\) and \(\lambda\), the eigenfunctions of a circular sector are
\[v(r,\theta) = J\left(\alpha, \sqrt{\lambda} r\right) \sin(\alpha \theta)\]
The eigenvalues are determined by the requirement that \(\theta = 0\) vanish on the boundary of the sector. For Pac-Man, the straight edges have \(v(r,θ)\) and \(\theta = 3\pi/2\), so we can satisfy the boundary conditions on these edges by choosing α to be an integer multiple of two-thirds,
\[\alpha_j = \frac{2j}{3}, \quad j \in \mathbb{Z}\]
The circular portion of the boundary has \(r = 1\), so we can satisfy the boundary conditions on the circle by taking \(\lambda\) to be a square of a zero of a Bessel function,
\[J(\alpha, \sqrt{\lambda}k = 0 \]
Contour plots of the first six eigenfunctions show that two are symmetric about the center line, \(\theta = 3\pi / 4\) two are antisymmetric about the center line, and two are eigenfunctions of the quarter disc, reflected twice to fill out the entire region. Linear combinations of these circular sector basis functions provide accurate approximations to the eigenvalues and eigenfunctions of other regions with corners. Let
\[v(r,\theta) = \sum_j c_j J\left(\alpha_j, \sqrt{\lambda} r\right) \sin(\alpha_j \theta)\]
These functions are exact solutions to the eigenvalue differential equation. They also satisfy the boundary conditions on the two edges that meet at the origin. All that remains is to pick \(\lambda\) and the \(c_j\)’s so that the boundary conditions on the remaining edges are satisfied.
A least squares approach employing the matrix singular value decomposition is used to determine \(\lambda\) and the \(c_j\)’s. Pick \(m\) points, \(r_i \theta_i\) on the remaining edges of the boundary. Let \(n\) be the number of fundamental solutions to be used. Define an m-by-n matrix \(A\) with elements that depend upon \(\lambda\),
\[A_{i,j} = J\left(\right) \sin(\alpha_j \theta_i), \quad i=1,\dots,m \text{ and } j=1,\ldots,n\]
Then, for any vector \(c\), the vector \(A_c\) is the vector of boundary values, \(v(r_i \theta_i)\). We want to make \(\|A_c\|\)|small without making \(\|c\|\) small. The SVD does this job. Let \(\sigma_n(A(\lambda))\) denote the smallest singular value of the matrix \(A(\lambda)\) and let \(\lambda_k\) denote the values of \(\lambda\) that produce local minima of the smallest singular value,
\[\lambda_k = \text{\(k\)-th minimizer }\sigma_n(A(\lambda))\]
Each \(\lambda_k\) approximates an eigenvalue of the region. The n-th column of the corresponding matrix \(V\) from the singular value decomposition provides the coefficient vector \(c\) for the linear combination.
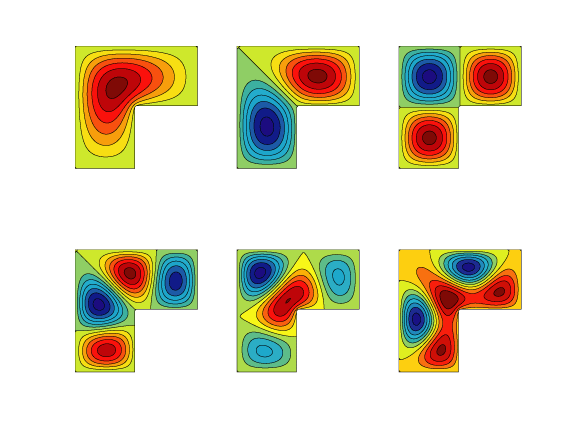
The MATLAB function membrane uses an older version of this algorithm to compute eigenfunctions of the L-shaped membrane. Contour plots of the first six eigenfunctions show that the first, fifth, and sixth are symmetric about the center line; the second and fourth are antisymmetric about the center line; and the third is actually the first eigenfunction of a unit square, reflected into the other two squares.
The MATLAB function logo generates our company logo, a lighted, reflective, surface plot of a variant of the first eigenfunction. After being so careful to satisfy the boundary conditions, the logo uses only the first two terms in the sum. This artistic license gives the edge of the logo a more interesting, curved shape.
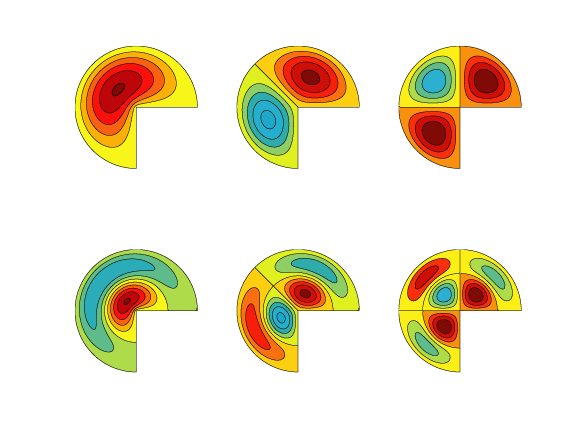
Published 2003