trimmean
Mean, excluding outliers
Syntax
Description
m = trimmean(X,percent)X, computed after removing the outliers
of X. For example, if X is a vector that has
n values, m is the mean of X
excluding the highest and lowest k data values, where k =
n*(percent/100)/2.
If
Xis a vector, thentrimmean(X,percent)is the mean of all the values ofX, computed after removing the outliers.If
Xis a matrix, thentrimmean(X,percent)is a row vector of column means, computed after removing the outliers.If
Xis a multidimensional array, thentrimmeanoperates along the first nonsingleton dimension ofX.
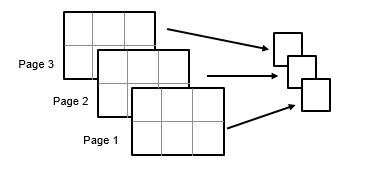
m = trimmean(___,vecdim)vecdim. For example, if X is a 2-by-3-by-4 array,
then trimmean(X,10,[1 2]) returns a 1-by-1-by-4 array. Each value of the
output array is the mean of the middle 90% of the values on the corresponding page of
X.
Examples
Input Arguments
Output Arguments
Tips
The trimmed mean is a robust estimate of the location of a data sample. If the data contains outliers, then the trimmed mean represents the center of the data better than the sample mean. However, if all the data is from the same probability distribution, then the trimmed mean is less efficient than the sample mean as an estimator of the data location.