azel2phitheta
Convert angles from azimuth-elevation form to phi-theta form
Description
PhiTheta = azel2phitheta(AzEl)
Examples
Convert Azimuth-Elevation Coordinates to Phi-Theta Coordinates
Find the phi-theta representation for 30° azimuth and 10° elevation for the convention where phi is defined from the y-axis to the z-axis, and theta is defined from the x-axis toward the yz-plane.
PhiTheta = azel2phitheta([30;10])
PhiTheta = 2×1
19.4254
31.4749
Azimuth-Elevation Coordinates to Alternative Phi-Theta Coordinates
Find the phi-theta representation for 30° azimuth and 10° elevation for the convention with phi defined from the x-axis to the y-axis, and theta defined from the z-axis toward the xy-plane.
PhiTheta = azel2phitheta([30;10],false)
PhiTheta = 2×1
30
80
Input Arguments
AzEl — Azimuth-elevation angle pairs
two-row matrix
Azimuth and elevation angles, specified as a two-row matrix. Each column of the matrix represents an angle in degrees, in the form [azimuth; elevation].
Data Types: double
RotAx — Phi-theta angle convention selection
true (default) | false
Phi-theta angle convention selection, specified as true
or false.
If
RotAxistrue, the phi angle is defined from the y-axis to the z-axis and the theta angle is defined from the x-axis toward the yz-plane.If
RotAxisfalse, the phi angle is defined from the x-axis to the y-axis and the theta angle is defined from the z-axis toward the xy- plane. (see Alternative Definition of Phi and Theta).
Data Types: double
Output Arguments
PhiTheta — Phi-theta angle pairs
two-row matrix
Phi and theta angles, returned as a two-row matrix. Each column of the
matrix represents an angle in degrees, in the form [phi; theta]. The matrix
dimensions of PhiTheta are the same as those of
AzEl.
More About
Azimuth and Elevation Angles
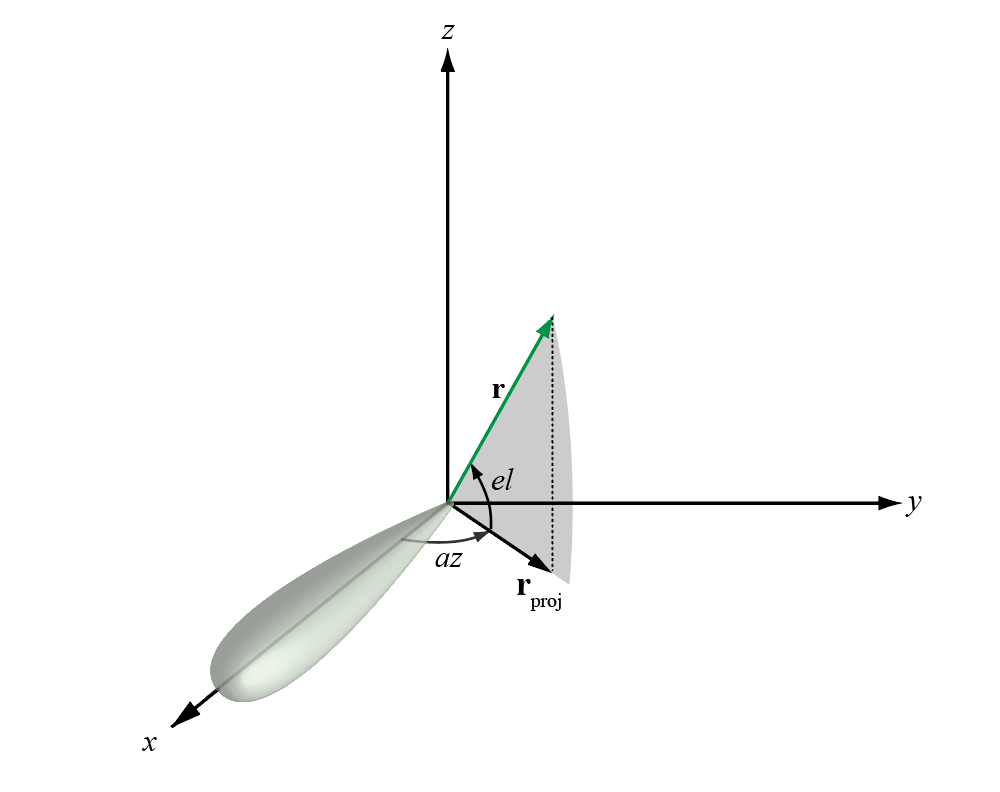
The azimuth angle of a vector is the angle between the x-axis and the orthogonal projection of the vector onto the xy plane. The angle is positive in going from the x axis toward the y axis. Azimuth angles lie between –180 and 180 degrees. The elevation angle is the angle between the vector and its orthogonal projection onto the xy-plane. The angle is positive when going toward the positive z-axis from the xy plane. By default, the boresight direction of an element or array is aligned with the positive x-axis. The boresight direction is the direction of the main lobe of an element or array.
Note
The elevation angle is sometimes defined in the literature as the angle a vector makes with the positive z-axis. The MATLAB® and Phased Array System Toolbox™ products do not use this definition.
This figure illustrates the azimuth angle and elevation angle for a vector shown as a green solid line.
Phi and Theta Angles
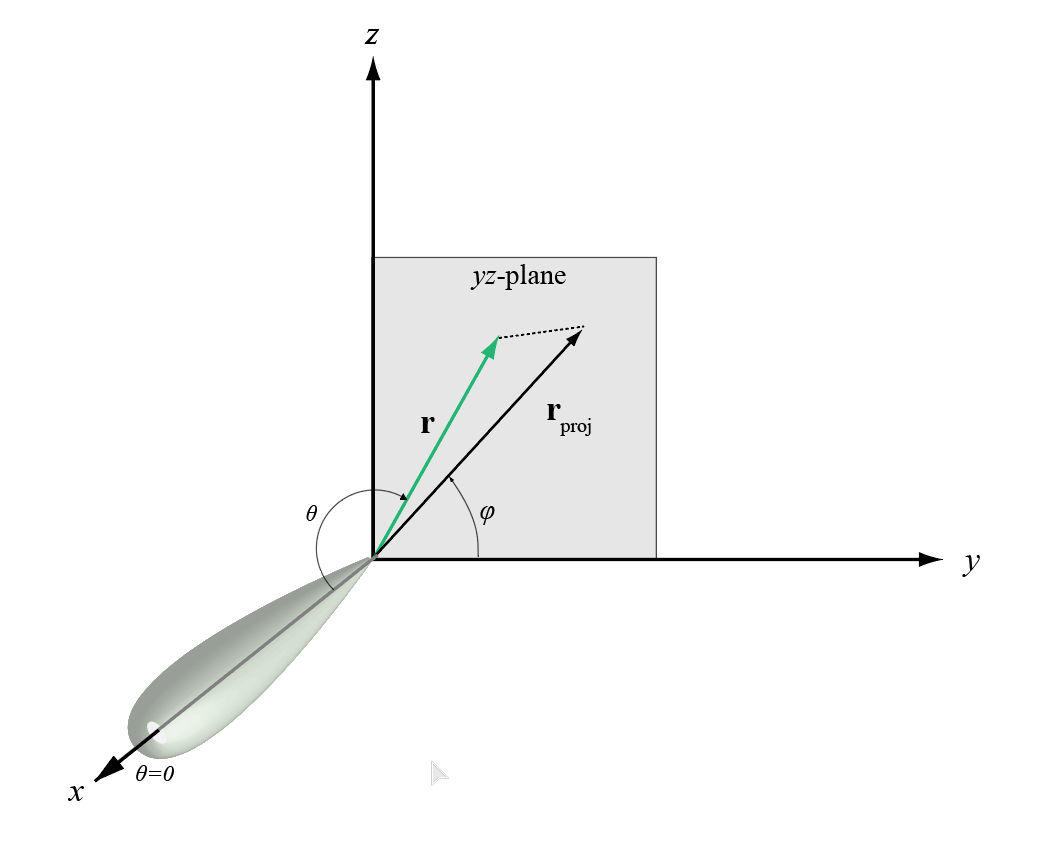
The phi angle (φ) is the angle from the positive y-axis to the vector’s orthogonal projection onto the yz plane. The angle is positive toward the positive z-axis. The phi angle is between 0 and 360 degrees. The theta angle (θ) is the angle from the x-axis to the vector itself. The angle is positive toward the yz plane. The theta angle is between 0 and 180 degrees.
The figure illustrates phi and theta for a vector that appears as a green solid line.
The coordinate transformations between φ/θ and az/el are described by the following equations
This transformation applies when RotAx is
true.
Alternative Definition of Phi and Theta
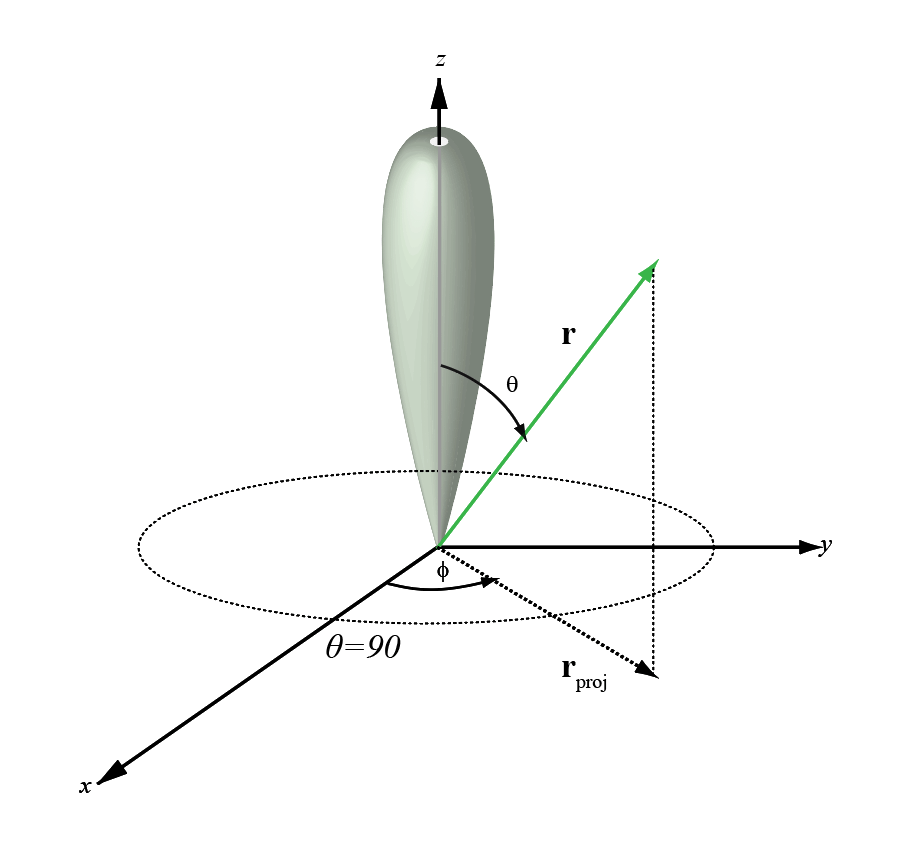
The phi angle (φ) is the angle from the positive x-axis to the vector’s orthogonal projection onto the xy plane. The angle is positive toward the positive y-axis. The phi angle is between 0 and 360 degrees. The theta angle (θ) is the angle from the z-axis to the vector itself. The angle is positive toward the xy plane. The theta angle is between 0 and 180 degrees.
The figure illustrates φ and θ for a vector that appears as a green solid line.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
Does not support variable-size inputs.
Version History
Introduced in R2012a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)