C Code Generation for a MATLAB Kalman Filtering Algorithm
This example shows how to generate C code for a MATLAB® Kalman filter function, kalmanfilter, which estimates the position of a moving object based on past noisy measurements. It also shows how to generate a MEX function for this MATLAB code to increase the execution speed of the algorithm in MATLAB.
Prerequisites
There are no prerequisites for this example.
About the kalmanfilter Function
The kalmanfilter function predicts the position of a moving object based on its past values. It uses a Kalman filter estimator, a recursive adaptive filter that estimates the state of a dynamic system from a series of noisy measurements. Kalman filtering has a broad range of application in areas such as signal and image processing, control design, and computational finance.
About the Kalman Filter Estimator Algorithm
The Kalman estimator computes the position vector by computing and updating the Kalman state vector. The state vector is defined as a 6-by-1 column vector that includes position (x and y), velocity (Vx Vy), and acceleration (Ax and Ay) measurements in a 2-dimensional Cartesian space. Based on the classical laws of motion:
The iterative formula capturing these laws are reflected in the Kalman state transition matrix "A". Note that by writing about 10 lines of MATLAB code, you can implement the Kalman estimator based on the theoretical mathematical formula found in many adaptive filtering textbooks.
type kalmanfilter.m% Copyright 2010 The MathWorks, Inc.
function y = kalmanfilter(z)
%#codegen
dt=1;
% Initialize state transition matrix
A=[ 1 0 dt 0 0 0;... % [x ]
0 1 0 dt 0 0;... % [y ]
0 0 1 0 dt 0;... % [Vx]
0 0 0 1 0 dt;... % [Vy]
0 0 0 0 1 0 ;... % [Ax]
0 0 0 0 0 1 ]; % [Ay]
H = [ 1 0 0 0 0 0; 0 1 0 0 0 0 ]; % Initialize measurement matrix
Q = eye(6);
R = 1000 * eye(2);
persistent x_est p_est % Initial state conditions
if isempty(x_est)
x_est = zeros(6, 1); % x_est=[x,y,Vx,Vy,Ax,Ay]'
p_est = zeros(6, 6);
end
% Predicted state and covariance
x_prd = A * x_est;
p_prd = A * p_est * A' + Q;
% Estimation
S = H * p_prd' * H' + R;
B = H * p_prd';
klm_gain = (S \ B)';
% Estimated state and covariance
x_est = x_prd + klm_gain * (z - H * x_prd);
p_est = p_prd - klm_gain * H * p_prd;
% Compute the estimated measurements
y = H * x_est;
end % of the function
Load Test Data
The position of the object to track are recorded as x and y coordinates in a Cartesian space in a MAT file called position_data.mat. The following code loads the MAT file and plots the trace of the positions. The test data includes two sudden shifts or discontinuities in position which are used to check that the Kalman filter can quickly re-adjust and track the object.
load position_data.mat
hold; grid;Current plot held
for idx = 1: numPts z = position(:,idx); plot(z(1), z(2), 'bx'); axis([-1 1 -1 1]); end title('Test vector for the Kalman filtering with 2 sudden discontinuities '); xlabel('x-axis');ylabel('y-axis'); hold;
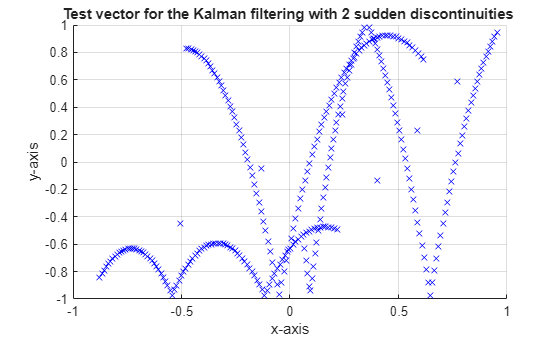
Current plot released
Inspect and Run the ObjTrack Function
The ObjTrack.m function calls the Kalman filter algorithm and plots the trajectory of the object in blue and the Kalman filter estimated position in green. Initially, you see that it takes a short time for the estimated position to converge with the actual position of the object. Then, three sudden shifts in position occur. Each time the Kalman filter readjusts and tracks the object after a few iterations.
type ObjTrack% Copyright 2010 The MathWorks, Inc.
function ObjTrack(position)
%#codegen
% First, setup the figure
numPts = 300; % Process and plot 300 samples
figure;hold;grid; % Prepare plot window
% Main loop
for idx = 1: numPts
z = position(:,idx); % Get the input data
y = kalmanfilter(z); % Call Kalman filter to estimate the position
plot_trajectory(z,y); % Plot the results
end
hold;
end % of the function
ObjTrack(position)
Current plot held Current plot released

Generate C Code
The codegen command with the -config:lib option generates C code packaged as a standalone C library.
Because C uses static typing, codegen must determine the properties of all variables in the MATLAB files at compile time. Here, the -args command-line option supplies an example input so that codegen can infer new types based on the input types.
The -report option generates a compilation report that contains a summary of the compilation results and links to generated files. After compiling the MATLAB code, codegen provides a hyperlink to this report.
z = position(:,1); codegen -config:lib -report -c kalmanfilter.m -args {z}
Code generation successful: To view the report, open('codegen/lib/kalmanfilter/html/report.mldatx')
Inspect the Generated Code
The generated C code is in the codegen/lib/kalmanfilter/ folder. The files are:
dir codegen/lib/kalmanfilter/. .. _clang-format buildInfo.mat codeInfo.mat codedescriptor.dmr compileInfo.mat examples html interface kalmanfilter.c kalmanfilter.h kalmanfilter_data.c kalmanfilter_data.h kalmanfilter_initialize.c kalmanfilter_initialize.h kalmanfilter_rtw.mk kalmanfilter_terminate.c kalmanfilter_terminate.h kalmanfilter_types.h rtw_proj.tmw rtwtypes.h
Inspect the C Code for the kalmanfilter.c Function
type codegen/lib/kalmanfilter/kalmanfilter.c/*
* File: kalmanfilter.c
*
* MATLAB Coder version : 24.1
* C/C++ source code generated on : 12-Feb-2024 20:59:29
*/
/* Include Files */
#include "kalmanfilter.h"
#include "kalmanfilter_data.h"
#include "kalmanfilter_initialize.h"
#include <math.h>
#include <string.h>
/* Variable Definitions */
static double x_est[6];
static double p_est[36];
/* Function Definitions */
/*
* Arguments : const double z[2]
* double y[2]
* Return Type : void
*/
void kalmanfilter(const double z[2], double y[2])
{
static const short R[4] = {1000, 0, 0, 1000};
static const signed char b_a[36] = {1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,
1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0,
0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1};
static const signed char iv[36] = {1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0,
0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1,
0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1};
static const signed char c_a[12] = {1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0};
static const signed char iv1[12] = {1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0};
double a[36];
double p_prd[36];
double B[12];
double Y[12];
double x_prd[6];
double S[4];
double b_z[2];
double a21;
double a22;
double a22_tmp;
double d;
int i;
int k;
int r1;
int r2;
signed char Q[36];
if (!isInitialized_kalmanfilter) {
kalmanfilter_initialize();
}
/* Copyright 2010 The MathWorks, Inc. */
/* Initialize state transition matrix */
/* % [x ] */
/* % [y ] */
/* % [Vx] */
/* % [Vy] */
/* % [Ax] */
/* [Ay] */
/* Initialize measurement matrix */
for (i = 0; i < 36; i++) {
Q[i] = 0;
}
/* Initial state conditions */
/* Predicted state and covariance */
for (k = 0; k < 6; k++) {
Q[k + 6 * k] = 1;
x_prd[k] = 0.0;
for (i = 0; i < 6; i++) {
r1 = k + 6 * i;
x_prd[k] += (double)b_a[r1] * x_est[i];
d = 0.0;
for (r2 = 0; r2 < 6; r2++) {
d += (double)b_a[k + 6 * r2] * p_est[r2 + 6 * i];
}
a[r1] = d;
}
}
for (i = 0; i < 6; i++) {
for (r2 = 0; r2 < 6; r2++) {
d = 0.0;
for (r1 = 0; r1 < 6; r1++) {
d += a[i + 6 * r1] * (double)iv[r1 + 6 * r2];
}
r1 = i + 6 * r2;
p_prd[r1] = d + (double)Q[r1];
}
}
/* Estimation */
for (i = 0; i < 2; i++) {
for (r2 = 0; r2 < 6; r2++) {
d = 0.0;
for (r1 = 0; r1 < 6; r1++) {
d += (double)c_a[i + (r1 << 1)] * p_prd[r2 + 6 * r1];
}
B[i + (r2 << 1)] = d;
}
for (r2 = 0; r2 < 2; r2++) {
d = 0.0;
for (r1 = 0; r1 < 6; r1++) {
d += B[i + (r1 << 1)] * (double)iv1[r1 + 6 * r2];
}
r1 = i + (r2 << 1);
S[r1] = d + (double)R[r1];
}
}
if (fabs(S[1]) > fabs(S[0])) {
r1 = 1;
r2 = 0;
} else {
r1 = 0;
r2 = 1;
}
a21 = S[r2] / S[r1];
a22_tmp = S[r1 + 2];
a22 = S[r2 + 2] - a21 * a22_tmp;
for (k = 0; k < 6; k++) {
double d1;
i = k << 1;
d = B[r1 + i];
d1 = (B[r2 + i] - d * a21) / a22;
Y[i + 1] = d1;
Y[i] = (d - d1 * a22_tmp) / S[r1];
}
for (i = 0; i < 2; i++) {
for (r2 = 0; r2 < 6; r2++) {
B[r2 + 6 * i] = Y[i + (r2 << 1)];
}
}
/* Estimated state and covariance */
for (i = 0; i < 2; i++) {
d = 0.0;
for (r2 = 0; r2 < 6; r2++) {
d += (double)c_a[i + (r2 << 1)] * x_prd[r2];
}
b_z[i] = z[i] - d;
}
for (i = 0; i < 6; i++) {
d = B[i + 6];
x_est[i] = x_prd[i] + (B[i] * b_z[0] + d * b_z[1]);
for (r2 = 0; r2 < 6; r2++) {
r1 = r2 << 1;
a[i + 6 * r2] = B[i] * (double)c_a[r1] + d * (double)c_a[r1 + 1];
}
for (r2 = 0; r2 < 6; r2++) {
d = 0.0;
for (r1 = 0; r1 < 6; r1++) {
d += a[i + 6 * r1] * p_prd[r1 + 6 * r2];
}
r1 = i + 6 * r2;
p_est[r1] = p_prd[r1] - d;
}
}
/* Compute the estimated measurements */
for (i = 0; i < 2; i++) {
d = 0.0;
for (r2 = 0; r2 < 6; r2++) {
d += (double)c_a[i + (r2 << 1)] * x_est[r2];
}
y[i] = d;
}
}
/*
* Arguments : void
* Return Type : void
*/
void kalmanfilter_init(void)
{
int i;
for (i = 0; i < 6; i++) {
x_est[i] = 0.0;
}
/* x_est=[x,y,Vx,Vy,Ax,Ay]' */
memset(&p_est[0], 0, 36U * sizeof(double));
}
/*
* File trailer for kalmanfilter.c
*
* [EOF]
*/
Accelerate the Execution Speed of the MATLAB Algorithm
You can accelerate the execution speed of the kalmanfilter function that is processing a large data set by using the codegen command to generate a MEX function from the MATLAB code.
Call the kalman_loop Function to Process Large Data Sets
First, run the Kalman algorithm with a large number of data samples in MATLAB. The kalman_loop function runs the kalmanfilter function in a loop. The number of loop iterations is equal to the second dimension of the input to the function.
type kalman_loop% Copyright 2010 The MathWorks, Inc.
function y=kalman_loop(z)
% Call Kalman estimator in the loop for large data set testing
%#codegen
[DIM, LEN]=size(z);
y=zeros(DIM,LEN); % Initialize output
for n=1:LEN % Output in the loop
y(:,n)=kalmanfilter(z(:,n));
end;
Baseline Execution Speed Without Compilation
Now time the MATLAB algorithm. Use the randn command to generate random numbers and create the input matrix position composed of 100,000 samples of (2x1) position vectors. Remove all MEX files from the current folder. Use the MATLAB stopwatch timer (tic and toc commands) to measure how long it takes to process these samples when running the kalman_loop function.
clear mex delete(['*.' mexext]) position = randn(2,100000); tic, kalman_loop(position); a=toc;
Generate a MEX Function for Testing
Next, generate a MEX function using the command codegen followed by the name of the MATLAB function kalman_loop. The codegen command generates a MEX function called kalman_loop_mex. You can then compare the execution speed of this MEX function with that of the original MATLAB algorithm.
codegen -args {position} kalman_loop.m
Code generation successful.
which kalman_loop_mex/tmp/Bdoc24a_2528353_313099/tp05579b37/coder-ex53054096/kalman_loop_mex.mexa64
Time the MEX Function
Now, time the MEX function kalman_loop_mex. Use the same signal position as before as the input, to ensure a fair comparison of the execution speed.
tic, kalman_loop_mex(position); b=toc;
Comparison of the Execution Speeds
Notice the speed execution difference using a generated MEX function.
display(sprintf('The speedup is %.1f times using the generated MEX over the baseline MATLAB function.',a/b));The speedup is 13.7 times using the generated MEX over the baseline MATLAB function.
