Rayleigh Distribution
Definition
The Rayleigh pdf is
Background
The Rayleigh distribution is a special case of the Weibull distribution. If A and B are the parameters of the Weibull distribution, then the Rayleigh distribution with parameter b is equivalent to the Weibull distribution with parameters and B = 2.
If the component velocities of a particle in the x and y directions are two independent normal random variables with zero means and equal variances, then the distance the particle travels per unit time is distributed Rayleigh.
In communications theory, Nakagami distributions, Rician distributions, and Rayleigh distributions are used to model scattered signals that reach a receiver by multiple paths. Depending on the density of the scatter, the signal will display different fading characteristics. Rayleigh and Nakagami distributions are used to model dense scatters, while Rician distributions model fading with a stronger line-of-sight. Nakagami distributions can be reduced to Rayleigh distributions, but give more control over the extent of the fading.
Parameters
The raylfit function returns the MLE of the Rayleigh parameter.
This estimate is
Examples
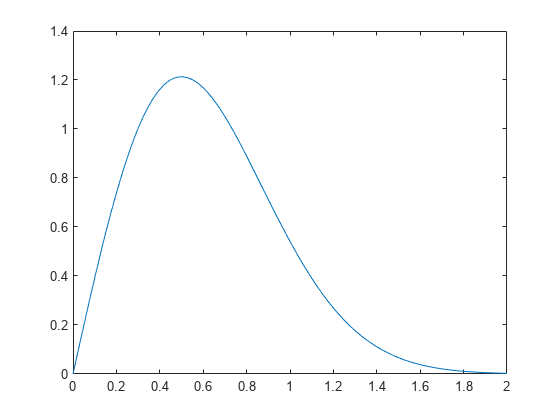
Compute and Plot Rayleigh Distribution pdf
Compute the pdf of a Rayleigh distribution with parameter B = 0.5.
x = [0:0.01:2]; p = raylpdf(x,0.5);
Plot the pdf.
figure; plot(x,p)