Fuel Cell
Libraries:
Simscape /
Electrical /
Sources
Description
The Fuel Cell block models a fuel cell that converts the chemical energy of hydrogen into electrical energy.
This chemical reaction defines the electrical conversion:
which occurs due to these anode and cathode half-reactions:

A fuel cell stack comprises several series-connected fuel cells. This figure shows the equivalent circuit of a single fuel cell that this block uses

where:
VFC is the cell voltage.
Ri is the Internal resistance.
Rd is the Sum of activation and concentration resistances.
Cdl is the parallel RC capacitance that accounts for time dynamics in the cell.
Equations
You can use the Model fidelity parameter to set the Fuel Cell block to two different levels of fidelity:
Simplified - nominal conditions— The block calculates the Nernst voltage at the nominal condition of temperature and pressure.Detailed with physical inputs— The block calculates the Nernst voltage by considering the pressures and flow rates of fuel and air.
When Model fidelity is set to Simplified - nominal
conditions, the Fuel Cell block
calculates the Nernst voltage, E, at the nominal condition of
temperature and pressure, as defined by these equations:
where:
Eoc is the Open-circuit voltage.
N is the Number of cells per module.
iFC is the current that the fuel cell generates.
vFC is the voltage across the fuel cell terminals.
Nunit is the Module units (Series).
vd is the voltage drop that accounts for fuel cell dynamics.
A is the Tafel slope, in volts.
i0 is the Nominal exchange current.
.
When Model fidelity is set to Detailed with physical
inputs, the Fuel Cell block
calculates the Nernst voltage, E, by considering the
pressures and flow rates of fuel and air.
These equations determine the rates of utilization of hydrogen, UH2, and oxygen, UO2
where:
Ve is the thermal voltage at room temperature.
pfuel is the supply pressure of the fuel, in
bar.qfuel is the fuel flow rate.
xH2 is the concentration of hydrogen in the fuel, in percent.
pair is the supply pressure of air, in
bar.qair is the air flow rate.
xO2 is the concentration of oxygen in the air, in percent.
These equations define the partial pressures:
where xH2O is the concentration of vapor in air, in percent.
Then, the block computes the Nernst voltage as

where:
.
is the electrokinetic term for the activation.
is the electrokinetic term for the concentration.
.
Kc is the voltage constant at nominal condition of operation.
T is the operating temperature of the fuel cell.
Tnom is the value of the Nominal temperature parameter.
z is the number of moving electrons per second.
z0 is the number of moving electrons per second at the value of the Nominal exchange current parameter.
F is the Faraday constant.
R is the universal gas constant.
pnH2 is the nominal hydrogen pressure, in
bar.pnO2 is the nominal oxygen pressure, in
bar.is the Tafel slope as a function of the temperature.
ilim is the value of the Collapse current parameter.
The voltage
1.229represents the standard cell potential for the Nernst equation.
The block computes the power dissipated, or the heat released in the fuel cell, by using this equation
where:
is the total electron circulation rate, in
mol/s.TΔS is the change in entropy of the fuel cell reaction, in
kJ/(mol*K), at the operating temperature of the fuel cell.ΔG is the change in Gibbs free energy of the full fuel cell reaction, in
kJ/mol, at the operating temperature of the fuel cell.
Variables
To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.
Use nominal values to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources. One of these sources is the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.
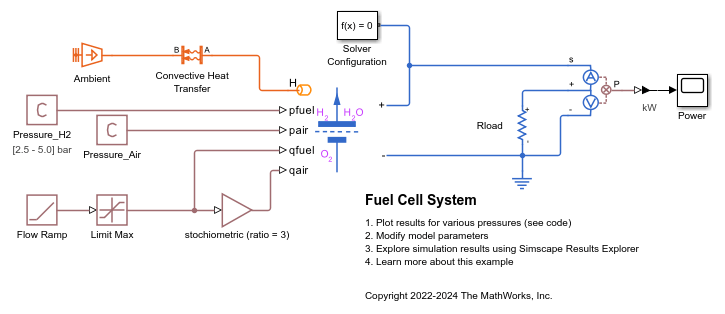
Examples
Limitations
The Fuel Cell block does not allow electrolysis.
Ports
Input
Conserving
Parameters
References
[1] Do, T.C., et al. “Energy Management Strategy of a PEM Fuel Cell Excavator with a Supercapacitor/Battery Hybrid Power Source”. Energies 12, no. 22, (November 2019). DOI.org (Crossref), doi:10.3390/en13010136.
[2] Motapon, Souleman N., O. Tremblay and L. Dessaint, “A generic fuel cell model for the simulation of fuel cell vehicles.” 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, 2009, pp. 1722-1729, doi: 10.1109/VPPC.2009.5289692
[3] Hirschenhofer, J. H.,, D.B. Stauffer, R.R. Engleman, and M.G. Klett. Fuel Cell Handbook (4th Ed). U.S. Department of Energy Office of Fossil Energy, 1988.
[4] Larminie, James, and Andrew Dicks. Fuel Cell Systems Explained. West Sussex, England: John Wiley & Sons, Ltd,., 2003. https://doi.org/10.1002/9781118878330.
Extended Capabilities
Version History
Introduced in R2021a