Manage Model Data to Simplify the Analysis
Simplify Data Types
One way to simplify your model is to use for the designated
signal data type a data type requiring the least amount of space for
the expected data. For example, do not use an int data
type for Boolean data, because only one bit is required for Boolean
data.
In another example, suppose you have a Sum block
with two inputs that are always
integers between –10 and 10. Set the Output data
type parameter to int8, rather
than int32 or double.
To display the signal data types, on the Debug tab, click Information Overlays > Port Data Type.
Constrain Data
Another effective technique for reducing complexity is to restrict the inputs to a set of representative values or, ideally, a single constant value. This process, called discretization, treats the input as if it were an enumeration. Discretization allows you to handle nonlinear arithmetic from multiplication and division in the simplest way possible.
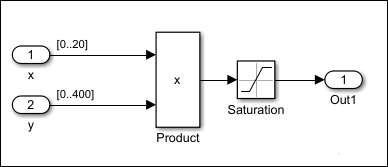
The following model has a Product block feeding a Saturation
block. The inputs x and y have specific design
ranges as shown and the Saturation block limits the input signal to
the upper and lower saturation values which is 8000 and 0 RPM.
The Simulink® Design Verifier™ software generates errors when attempting to satisfy the upper and lower limits of the Saturation block, because the software does not support nonlinear arithmetic. To work around these errors, restrict one of the inputs to a set of discrete values.
Identify discrete values that are required to satisfy your testing needs. For example, you may have an input for model speed, and your design contains paths of execution that are conditioned on speed above or below thresholds of 80, 150, 600, and 8000 RPM. For an effective analysis, constrain speed values to be 50, 100, 200, 1000, 5000, or 10000 RPM so that every threshold can be either active or inactive.
If you need to use more than two or three values, consider specifying the constrained values using an expression like
num2cell(minval:increment:maxval)
Using the previous example model, restrict the second input
(y) to be either 1, 2, 5,
or 10 using the Test Condition block as shown in
the following model. The Simulink
Design Verifier software produces
test cases for all inputs.

You can also constrain signals that are intermediate or output values of the model. Constraining such signals makes it easier to work around multiplication or division inside lower level subsystems that do not depend on model inputs.
Note
Discretization is best limited to a small number of inputs (less than 10). If your model requires discretization of many inputs, try to achieve model coverage through successive simulations, as described in Partition Model Inputs for Incremental Test Generation.
Test Condition blocks do not need to be placed exactly on the inputs. In deciding where to place the constraints in your model, consider the following guidelines:
Favor constraints on the input values because the software can process inputs easier.
If you need to place constraints on both the input and the output, for example, to avoid nonlinear arithmetic, one of the constraints should be a range such as
[minval maxval]. The software first tests the values at both ends of the range and can return a test case, even if the underlying calculations are nonlinear.Make sure that constraints at corresponding input and output points are not contradictory. Do not constrain the output signals to values that are not achievable because of the constraints on the input values.
Avoid creating constraints that contradict the model. Such contradictions occur when a constraint can never be satisfied because it contradicts some aspect of the model or another constraint. Analyzing contradictory models can cause Simulink Design Verifier to hang.
The next model is a simple example of a contradictory model. The second input to the Multiply block is the constant
1, but the Test Condition block constrains it to a value of2,5, or10. The analysis cannot achieve all the test objectives in this model.
When you work with large models that have many multiplication and division operations, you may find it easier to add constraints to all of the floating-point inputs rather than to identify the precise set of inputs that require constraints.