Enforce Barrier Certificate Constraints for Adaptive Cruise Control
This example shows how to enforce barrier certificate constraints for adaptive cruise control (ACC) using the Barrier Certificate Enforcement block.
Overview
In this example, the goal is to make an ego car travel at a set velocity while maintaining a safe distance from a lead car by controlling longitudinal acceleration and braking.
Configure model parameters.
x0_lead = 52; % Initial position for lead car (m) v0_lead = 25; % Initial velocity for lead car (m/s) x0_ego = 10; % Initial position for ego car (m) v0_ego = 20; % Initial velocity for ego car (m/s) default_spacing = 10; % Default spacing (m) time_gap = 1.5; % Time gap (s) v_set = 30; % Driver-set velocity (m/s) min_ac = -3; % Minimum acceleration for driver comfort (m/s^2) max_ac = 2; % Maximum acceleration for driver comfort (m/s^2) Ts = 0.1; % Sample time (s) T = 80; % Duration (s)
Open the model.
mdl = 'barrierCertificateACC';
open_system(mdl)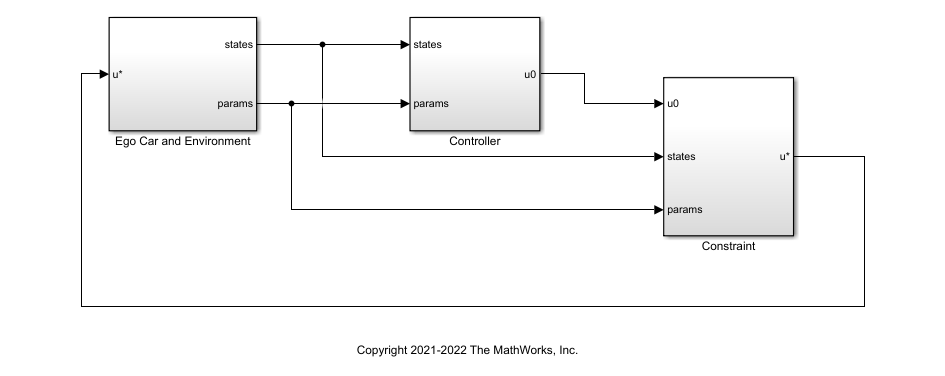
Controller Design
The controller design for ACC is based on the following principles.
If the relative distance is less than the safe distance, then the primary goal is to slow down and maintain a safe distance.
If the relative distance is greater than the safe distance, then the primary goal is to reach the driver-set velocity while maintaining a safe distance.
The safe distance is defined as a function of velocity.
Here:
is the default spacing.
is the time gap.
is the longitudinal velocity of the ego vehicle.
For an example that applies the same controller structure and design principles, see Adaptive Cruise Control System Using Model Predictive Control (Model Predictive Control Toolbox).
Specify the gains.
verr_gain = 0.5; % ACC velocity error gain xerr_gain = 0.1; % ACC spacing error gain vx_gain = 0.2; % ACC relative velocity gain
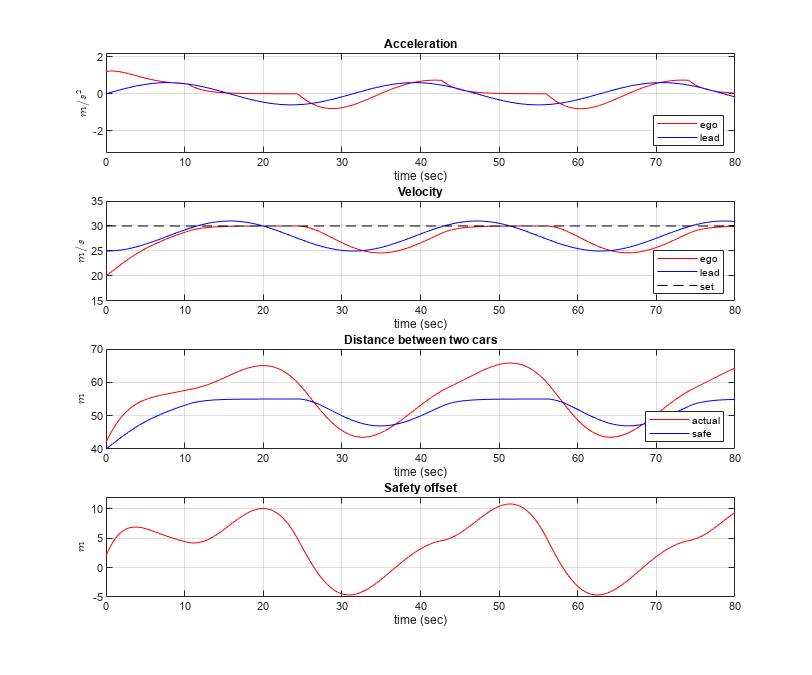
Before you apply any constraints, run the Simulink® model and view the results.
constrained = 0; sim(mdl); accPlotResults(logsout,default_spacing,time_gap,v_set);
Barrier Certificate Constraints
For the ACC application, the safety set is defined as the relative distance . Therefore, the barrier certificate is given by the safety offset .
The plant dynamics are described by the following equations.
Here, is the position for the ego car and is the velocity for lead car.
The barrier certificate is a function of states and is given by . The partial derivative of over states is given by .
The Barrier Certificate Enforcement block accepts plant dynamics in the form . For this application, and .
Simulate ACC Controller with Barrier Certificate Constraint
To view the constraint implementation, open the Constraint > Constrained subsystem.
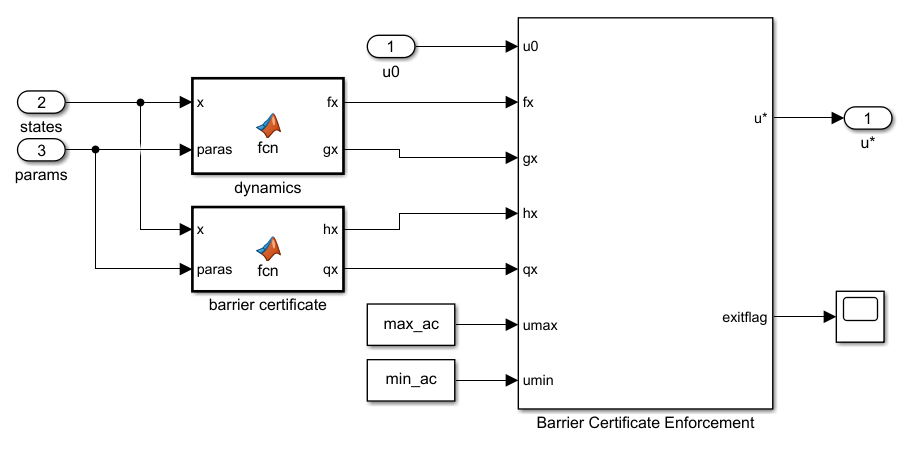
Enable the constraints.
constrained = 1;
Run the model and plot the simulation results.
sim(mdl); accPlotResults(logsout,default_spacing,time_gap,v_set);

The plot shows that the barrier certificate (safety offset) is nonnegative. The relative distance is always greater than the defined safe distance.
The Barrier Certificate Enforcement block successfully constrains the control actions such that the relative distance is greater than the safe distance.
Close the model.
bdclose(mdl)
See Also
Barrier Certificate Enforcement