Choose a Solver
To simulate a dynamic system, you compute its states at successive time steps over a specified time span. This computation uses information provided by a model of the system. Time steps are time intervals when the computation happens. The size of this time interval is called step size. The process of computing the states of a model in this manner is known as solving the model. No single method of solving a model applies to all systems. Simulink® provides a set of programs called solvers. Each solver embodies a particular approach to solving a model.
A solver applies a numerical method to solve the set of ordinary differential equations that represent the model. Through this computation, it determines the time of the next simulation step. In the process of solving this initial value problem, the solver also satisfies the accuracy requirements that you specify.
Mathematicians have developed a wide variety of numerical integration techniques for solving the ordinary differential equations (ODEs) that represent the continuous states of dynamic systems. An extensive set of fixed-step and variable-step continuous solvers are provided, each of which implements a specific ODE solution method (see Compare Solvers). Select solvers in the Solver pane of model configuration parameters.
All solvers provided by MATLAB® and Simulink follow a similar naming convention: ode, followed by two or
three numerals indicating the orders of the solver. Some solvers can solve stiff
differential equations and the methods used by them are expressed by the
s, t, or tb suffixes.
Automatic Solver Selection
When you specify the Solver and Max step
size parameters as auto, the software uses an
algorithm to select a solver and maximum step size value. For most models, the software
can select an appropriate solver and step size.
The algorithm uses several heuristics to select the solver based on model characteristics. The chart illustrates some heuristics for the selection algorithm.
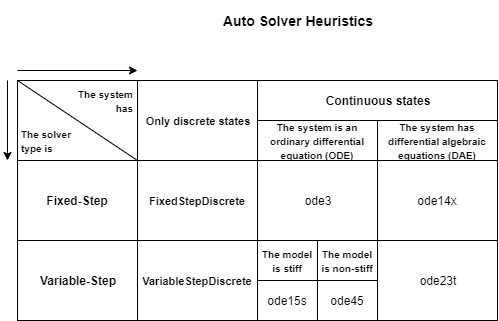
When the model contains only discrete states, the software selects the discrete solver for the specified solver type.
For a fixed-step solver, the software selects the discrete fixed-step solver.
For a variable-step solver, the software selects the discrete variable-step solver.
When the model contains continuous states, the solver selection depends on the solver type and the mathematical representation of the model.
For a fixed-step solver for a system that can be represented using ODEs, the software selects the
ode3solver.For a fixed-step solver for a model of a system that can be represented as a system of differential algebraic equations (DAEs), the software selects the
ode14xsolver.For a variable-step solver for a system that can be represented using ODEs, the software selects the solver based on the stiffness of the model.
For stiff models, the software selects the
ode15ssolver.For models that are not stiff, the software selects the
ode45solver.
For a variable-step solver for a system that can be represented using DAEs, the software selects the
ode23tsolver.
The software calculates the stiffness of the model when the number of continuous
states is less than the value of the NumStatesForStiffnessChecking
parameter. By default, the NumStatesForStiffnessChecking parameter
value is 1000.
When the number of continuous states in the model exceeds the value of the
NumStatesForStiffnessChecking parameter, the software considers
the model as stiff without calculating the stiffness and selects the
ode15s solver.
When the number of continuous states in the model is less than the value of the
NumStatesForStiffnessChecking parameter, the software calculates
the system stiffness to select a solver based on the value of the
StiffnessThreshold parameter.
When the calculated stiffness is less than the value of the
StiffnessThresholdparameter, the software considers the model not stiff and selects theode45solver.When the calculated stiffness is greater than the value of the
StiffnessThresholdparameter, the software considers the model stiff and selects theode15ssolver.
The default value for the NumStatesForStiffnessChecking and
StiffnessThreshold parameters is 1000. You can
specify a different value for either parameter using the set_param
function.
For Simscape™
Electrical™ models, the software selects the solver ode23tb.
Systems modeled using Simscape
Electrical can include nonlinear circuit components, such as circuit breakers and
power electronics, that require a stiff solver.
Solver Selection Criteria
The appropriate solver for simulating a model depends on these characteristics:
System dynamics
Solution stability
Computation speed
Solver robustness
As such, the numerical solvers provided by Simulink can be broadly classified by two properties.
Computation Step Size Type
Fixed-step solvers, as the name suggests, solve the model using the same step size from the beginning to the end of the simulation. You can specify the step size or let the solver choose it. Generally, decreasing the step size increases the accuracy of the results and the time required to simulate the system.
Variable-step solvers vary the step size during the simulation. These solvers reduce the step size to increase accuracy at certain events during the simulation of the model, such as rapid state changes, zero-crossing events, etc. Also, they increase the step size to avoid taking unnecessary steps when the states of a model change slowly. Computing the step size adds to the computational overhead at each step. However, it can reduce the total number of steps, and hence the simulation time required to maintain a specified level of accuracy for models with zero-crossings, rapidly changing states, and other events requiring extra computation.
Model States
Continuous solvers use numerical integration to compute continuous states of a model at the current time step based on the states at previous time steps and the state derivatives. Continuous solvers rely on individual blocks to compute the values of the discrete states of the model at each time step.
Discrete solvers are primarily used for solving purely discrete models. They compute only the next simulation time step for a model. When they perform this computation, they rely on each block in the model to update its individual discrete state. They do not compute continuous states.
Use an iterative approach to choose a solver for your requirements. Compare simulation results from several solvers and select a solver that offers the best performance with minimal tradeoffs.
Select a solver for your model in these ways:
Use auto solver. New models have their solver selection set to auto solver by default. Auto solver recommends a fixed-step or variable-step solver for your model as well as the maximum step size.
If you are not satisfied with the simulation results using auto solver, select a solver in the Solver pane in the model configuration parameters.
When you build and simulate a model, you can choose the solver based on the dynamics of your model. A variable-step solver is better suited for purely continuous models, like the dynamics of a mass spring damper system. A fixed-step solver is recommended for a model that contains several switches, like an inverter power system, due to the number of solver resets that would cause a variable-step solver to behave like a fixed-step solver.
Note
When you deploy a model as generated code, you can use only a fixed-step solver. If you select a variable-step solver during simulation, use it to calculate the step size required for the fixed-step solver that you need at deployment.
This chart provides a broad classification of solvers in the Simulink library.

To tailor the selected solver to your model, see Check and Improve Simulation Accuracy.
Ideally, the solver you select should:
Solve the model successfully.
For variable-step solvers, provide a solution within the tolerance limits you specify.
Solve the model in a reasonable duration.
A single solver might not meet all of these goals. Try simulating using different solvers before making a selection.
The Simulink library provides several solvers, all of which can work with the algebraic loop solver. For more information, see How the Algebraic Loop Solver Works.
| Solver Type | Explicit/Implicit | Discrete | Continuous | Variable-Order |
|---|---|---|---|---|
| Fixed-Step | Explicit | Not Applicable | Fixed-Step Continuous Explicit Solvers | Not Applicable |
| Implicit | Not Applicable | Fixed-Step Continuous Implicit Solvers | Not Applicable | |
| Variable-Step | Explicit | Variable Step Solvers in Simulink | Variable-Step Continuous Explicit Solvers | Single-Order Versus Variable-Order Continuous Solvers |
| Implicit | Variable-Step Continuous Implicit Solvers | Single-Order Versus Variable-Order Continuous Solvers |
In the Solver pane of model configuration parameters, the Simulink library of solvers is divided into two major types. See Fixed-Step Versus Variable-Step Solvers.
For other ways to compare solvers, see:
