Kaiser Window
The Kaiser window is an approximation to the prolate spheroidal window, for which the ratio of
the mainlobe energy to the sidelobe energy is maximized. For a Kaiser window of a
particular length, the parameter β controls the relative
sidelobe attenuation. For a given β, the relative sidelobe
attenuation is fixed with respect to window length. The statement kaiser(n,beta) computes a
length n Kaiser window with parameter
beta.
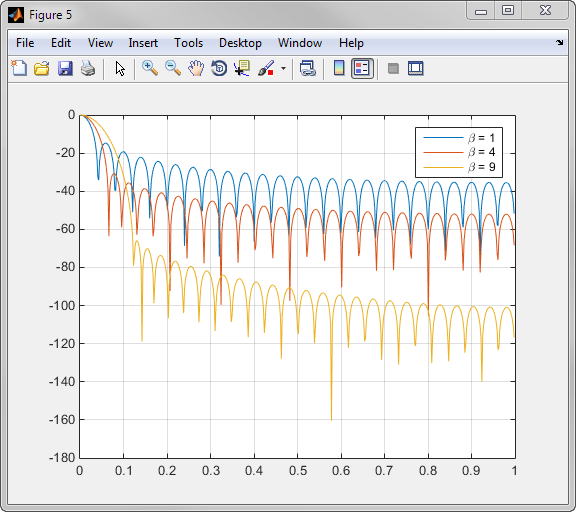
As β increases, the relative sidelobe attenuation decreases and the mainlobe width increases. This screen shot shows how the relative sidelobe attenuation stays approximately the same for a fixed β parameter as the length is varied.
Examples of Kaiser windows with length 50 and β parameters of 1, 4, and 9 are shown in this example.

To create these Kaiser windows using the MATLAB® command line, type the following:
n = 50; w1 = kaiser(n,1); w2 = kaiser(n,4); w3 = kaiser(n,9); [W1,f] = freqz(w1/sum(w1),1,512,2); [W2,f] = freqz(w2/sum(w2),1,512,2); [W3,f] = freqz(w3/sum(w3),1,512,2); plot(f,20*log10(abs([W1 W2 W3]))) grid legend('\beta = 1','\beta = 4','\beta = 9')

To create these Kaiser windows using the MATLAB command line, type the following:
w1 = kaiser(50,4); w2 = kaiser(20,4); w3 = kaiser(101,4); [W1,f] = freqz(w1/sum(w1),1,512,2); [W2,f] = freqz(w2/sum(w2),1,512,2); [W3,f] = freqz(w3/sum(w3),1,512,2); plot(f,20*log10(abs([W1 W2 W3]))) grid legend('length = 50','length = 20','length = 101')

Kaiser Windows in FIR Design
There are two design formulas that can help you design FIR filters to meet a set of filter specifications using a Kaiser window. To achieve a relative sidelobe attenuation of –α dB, the β (beta) parameter is
For a transition width of rad/sample, use the length
.
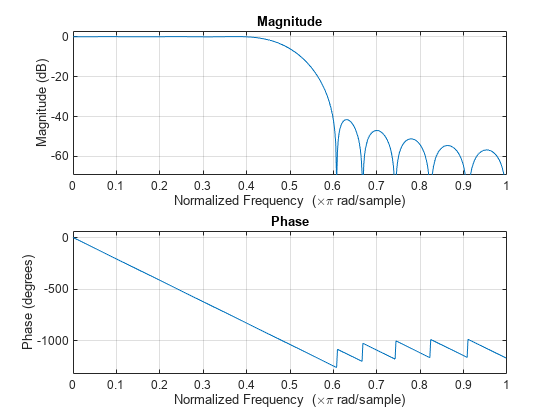
Filters designed using these heuristics will meet the specifications approximately, but you should verify this. To design a lowpass filter with cutoff frequency 0.5 rad/sample, transition width 0.2 rad/sample, and 40 dB of attenuation in the stopband, try
[n,wn,beta] = kaiserord([0.4 0.6]*pi,[1 0],[0.01 0.01],2*pi);
h = fir1(n,wn,kaiser(n+1,beta),'noscale');The kaiserord function estimates the filter order, cutoff frequency, and Kaiser window beta parameter needed to meet a given set of frequency domain specifications.
The ripple in the passband is roughly the same as the ripple in the stopband. As you can see from the frequency response, this filter nearly meets the specifications:
freqz(h,1)