Retune the Drive Parameters
This example shows how to modify the parameters of an electric drive using the AC3 drive model. In this example, the nominal power of the motor changes from 200 hp to 5 hp. To retune the drive parameters:
Modify Motor Parameters
Open the example:
ac3_example. Typeac3_examplein the MATLAB® Command Window.The parameters are set for a 200 hp motor.
Simulate the model in Accelerator mode and observe the results.
Double-click the Field-Oriented Control Induction Motor Drive block and select the Asynchronous Machine tab. Copy these parameters of the 5 hp motor into the drive's mask.
Parameter Value Reference frame RotorDiscrete solver model Forward EulerElectrical parameters > Nominal values > Power 3730Electrical parameters > Nominal values > Voltage 460Electrical parameters > Nominal values > Frequency 60Electrical parameters > Equivalent circuit values > Main winding stator > Resistance 1.115Electrical parameters > Equivalent circuit values > Main winding stator > Leakage inductance 0.005974Electrical parameters > Equivalent circuit values > Main winding stator > Mutual inductance 0.2037Electrical parameters > Equivalent circuit values > Main winding rotor > Resistance 1.083Electrical parameters > Equivalent circuit values > Main winding rotor > Leakage inductance 0.005974Electrical parameters > Initial Currents > Ia_Magnitude 0Electrical parameters > Initial Currents > Ia_Phase 0Electrical parameters > Initial Currents > Ib_Magnitude 0Electrical parameters > Initial Currents > Ib_Phase 0Electrical parameters > Initial Currents > Ic_Magnitude 0Electrical parameters > Initial Currents > Ic_Phase 0Mechanical parameters > Inertia 0.02Mechanical parameters > Friction factor 0.005752Mechanical parameters > Pole pairs 2Initial values > Slip 1Initial values > Angle 0
Retune Parameters of the Flux Regulator
To measure the signals associated to the flux regulator, add these blocks into the demux subsystem.
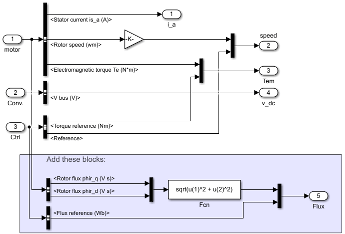
Select the Controller tab in the mask of the Field-Oriented Control Induction Motor Drive block. Set the Regulation type to
Torque regulationto access the controller parameters.The torque regulation mode is required to bypass the speed regulator parameters and act directly on the field-oriented control (FOC) controller.
The current controlled by the FOC controller depends of the machine flux. The flux controller ensures that the required flux is correctly applied to the machine.
Copy these parameters into the drive’s mask:
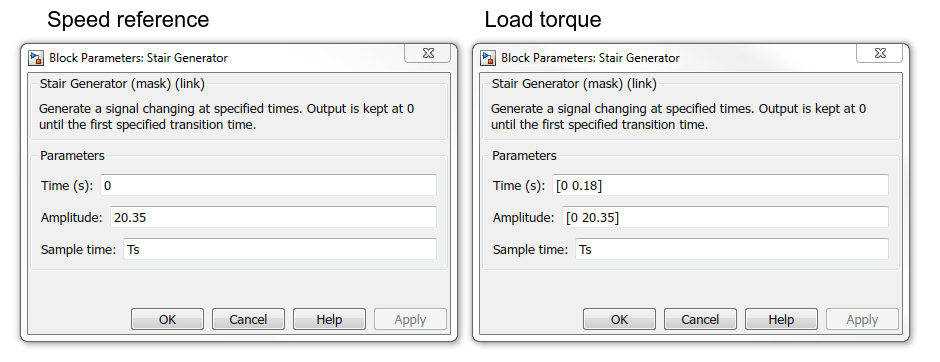
Parameter Value Machine flux > Initial 0.705Machine flux > Nominal 0.705Field oriented control > Flux controller > Proportional gain 1Field oriented control > Flux controller > Integral gain 0Field oriented control > Flux controller > Low-pass filter cutoff frequency 10e3Field oriented control > Flux controller > Flux output limits > Negative -0.705*1.5Field oriented control > Flux controller > Flux output limits > Positive 0.705*1.5Field oriented control > Current controller Hysteresis bandwidth 1To apply the nominal torque to the motor, modify the parameters of the Stair Generator blocks in the Speed reference subsystem and in the Load torque subsystem.
On the Logging tab of the Scope block, set Decimation to
1and Variable name tosimout1. Select Log data to workspace and set Save format toStructure With Time.Simulate the system for 0.5 s. Open the FFT Analysis tool of the powergui block.
In the Input list, select the
Stator currentsignal and set Start time to0.23, Number of cycles to1, Fundamental frequency to7.5, and Max Frequency (Hz) to20000Hz.Click Display to get the FFT graph.
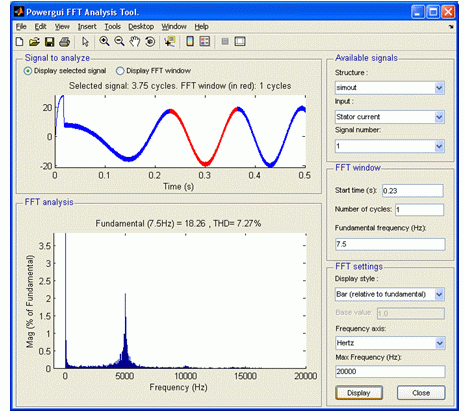
Note that the switching frequency is about 5 kHz. To attenuate this frequency, set the Flux controller Low-pass filter cutoff frequency parameter to 500 Hz.
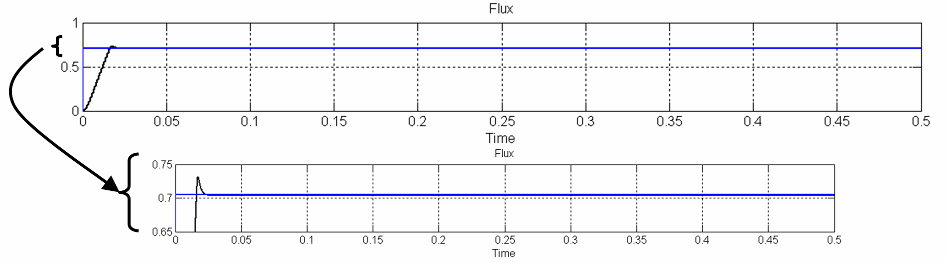
Open the Scope block and observe the flux signal. Note that the steady-state error is high.

Gradually increase the Flux controller Proportional gain parameter and simulate until you obtain a satisfactory response. Increasing the gain above a certain value can cause a saturation of the Flux controller. The curve at the next plot is based on a proportional gain of 100.

Gradually increase the Flux controller Integral gain and simulate until you obtain a satisfactory steady-state result with minimal error. The next plot is based on an integral gain of 90.
Retune Parameters of the Speed Regulator
Select the Controller tab in the mask of Field-Oriented Control Induction Motor Drive block and set the Regulation type to
Speed regulationto edit the controller parameters.Parameter Value Speed controller > Torque output limits> Negative -1200*1.5Speed controller > Torque output limits> Positive 1200*1.5Speed controller > PI regulator > Proportional gain 1Speed controller > PI regulator > Integral gain 0Speed controller > Speed cutoff frequency 500Field oriented control > Maximum switching frequency 500The speed ramp acceleration must be calculated to avoid exceeding the torque output limit. The required torque to accelerate the motor at 1750 rpm/s is given by:
To apply the nominal torque to the motor, modify the parameters of the Stair Generator blocks in the Speed reference subsystem and in the Load torque subsystem.
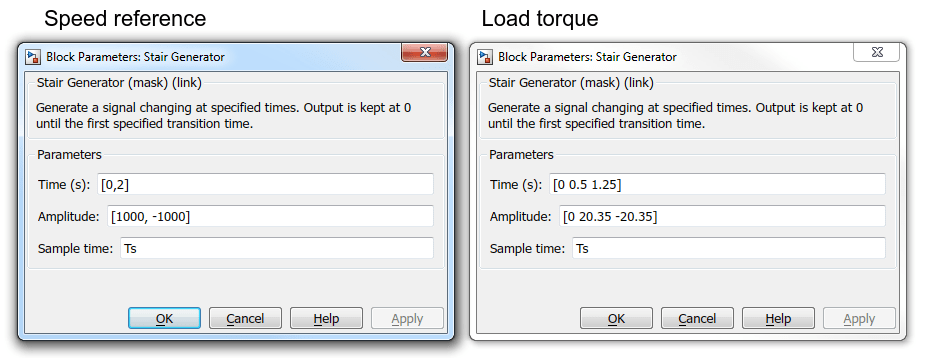
Set the scope decimation to 25 to prevent memory overload. Start the simulation.
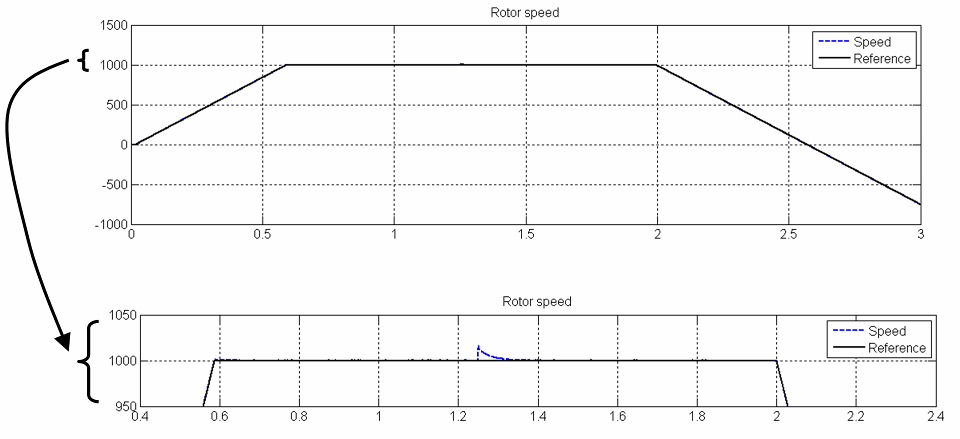
Observe the speed signal on the Scope block. The steady state error is high and the response time is not acceptable.

Gradually increase the Proportional gain parameter of the speed controller and simulate until you obtain a satisfactory response time without overshoot. Note that if the gain is too high, the system will be oscillatory. The next plot is based on a proportional gain of 3.

Gradually increase the Integral gain of the speed controller and simulate until you obtain a satisfactory steady state value with a minimal steady-state error. This curve is based on an integral gain of 100.
Retune Parameters of the DC Bus Voltage
Select the Converter and DC bus tab in the mask of the Field-Oriented Control Induction Motor Drive block to tune the DC bus capacitor and the braking chopper parameters.
Set the DC Bus Capacitance parameter to 167e-6.
The DC bus capacitance is calculated in order to reduce the voltage ripple.
where:
Pmotor is the nominal power of the motor drive (W).
f is the frequency of the AC source (Hz).
ΔV is the desired voltage ripple (V).
VDC is the average DC Bus voltage (V).
This equation gives an approximate value of the capacitor required for a given voltage ripple level. Here the desired voltage ripple is 50 V.
The motor drive of 5 hp (3728 W) is fed by a 60 Hz three-phase source. The average DC bus voltage is given by:
where VLL represents the line to line rms voltage of the source. The source line to line voltage is 460 Vrms so the DC voltage is VDC = 621 V.VDC = 1.35·VLL,
The required capacitor is then equal to
Set the Braking chopper Shutdown voltage to 660V and the Braking chopper Activation voltage to 700 V.
In motor mode, the peak voltage of the DC bus is equal to
The shutdown voltage (Vshut) of the braking chopper should be a little bit higher than this value. To limit the voltage increase during regenerative braking, shutdown voltage is set to 660 V, and the activation voltage (Vact) is set to 700 V.
Set the Braking chopper Resistance to 131 ohms.
The braking chopper resistance is calculated using this equation:
Simulate and Analyze the Results
Simulate the system and observe six sections of the simulation results.
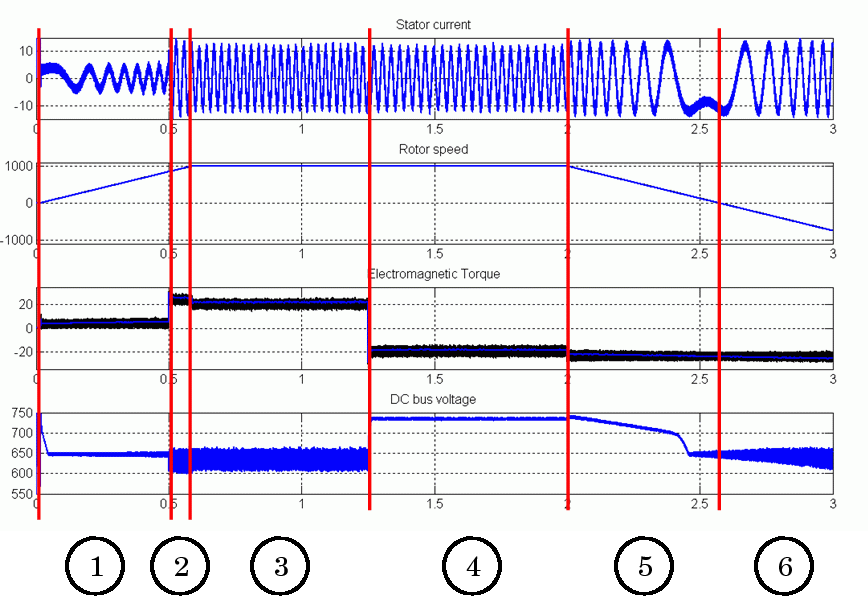
No-load acceleration
Nominal load torque is applied
Steady state speed
Nominal generation torque is applied: Observe the DC bus voltage overshoot
Deceleration
Negative speed acceleration
