Annular Leakage (IL)
Models annular leakage between a circular tube and a round insert in an isothermal flow
Since R2020a
Libraries:
Simscape /
Fluids /
Isothermal Liquid /
Valves & Orifices /
Orifices
Description
The Annular Leakage (IL) block models annular leakage between a circular tube and a round insert in an isothermal liquid network. The insert can be located off-center from the tube and can have varying lengthwise overlap with the tube.
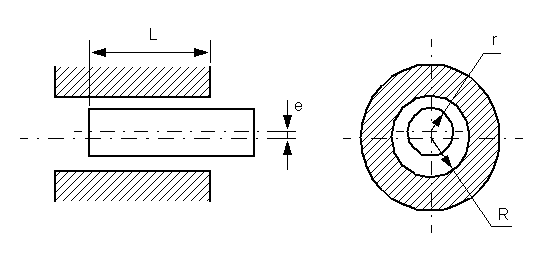
Ports A and B correspond with the orifice inlet and outlet. The input ports L and E are optional physical signal ports that model variable overlap length (L) and variable eccentricity (E).
The Mass Flow Rate Equation
The leakage mass flow rate is calculated from the pressure-flow rate equation
where:
R is the annulus outer radius.
r is the annulus inner radius.
pA is the pressure at port A.
pB is the pressure at port B.
ν is the fluid kinematic viscosity.
l is the overlap length.
ε is the eccentricity ratio, , where e is the eccentricity, which can be defined as a physical signal or constant value.
εsat is the saturated eccentricity ratio, which is ε for constant orifices, or the physical signal connected to port L for variable orifices. The eccentricity ratio is always between 0 and 1.
When modeling a variable overlap length, the user-defined minimum overlap length is used if the physical signal falls below the value of the Minimum overlap length parameter.
Assumptions and Limitations
The pressure-flow equation is valid only for fully-developed, laminar flows. The flow Reynolds number can be determined using or by checking the simulation log in the Results Explorer or the Simulation Data Inspector. For more information, see Data Logging.
Ports
Conserving
Input
Parameters
Extended Capabilities
Version History
Introduced in R2020a