Large Sparse Quadratic Program with Interior Point Algorithm
This example shows the value of using sparse arithmetic when you have a sparse problem. The matrix has n rows, where you choose n to be a large value, and a few nonzero diagonal bands. A full matrix of size n-by-n can use up all available memory, but a sparse matrix presents no problem.
The problem is to minimize x'*H*x/2 + f'*x subject to
x(1) + x(2) + ... + x(n) <= 0,
where f = [-1;-2;-3;...;-n]. H is a sparse symmetric banded matrix.
Create Sparse Quadratic Matrix
Create a symmetric circulant matrix based on shifts of the vector [3,6,2,14,2,6,3], with 14 being on the main diagonal. Have the matrix be n-by-n, where n = 30,000.
n = 3e4;
H2 = speye(n);
H = 3*circshift(H2,-3,2) + 6*circshift(H2,-2,2) + 2*circshift(H2,-1,2)...
+ 14*H2 + 2*circshift(H2,1,2) + 6*circshift(H2,2,2) + 3*circshift(H2,3,2);View the matrix structure.
spy(H)
Create Linear Constraint and Objective
The linear constraint is that the sum of the solution elements is nonpositive. The objective function contains a linear term expressed in the vector f.
A = ones(1,n); b = 0; f = 1:n; f = -f;
Solve Problem
Solve the quadratic programming problem using the 'interior-point-convex' algorithm. To keep the solver from stopping prematurely, set the StepTolerance option to 0.
options = optimoptions(@quadprog,'Algorithm','interior-point-convex','StepTolerance',0); [x,fval,exitflag,output,lambda] = ... quadprog(H,f,A,b,[],[],[],[],[],options);
Minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance. <stopping criteria details>
On many computers you cannot create a full n-by-n matrix when n = 30,000. So you can run this problem only by using sparse matrices.
Examine Solution
View the objective function value, number of iterations, and Lagrange multiplier associated with linear inequality.
fprintf('The objective function value is %d.\nThe number of iterations is %d.\nThe Lagrange multiplier is %d.\n',... fval,output.iterations,lambda.ineqlin)
The objective function value is -3.133073e+10. The number of iterations is 7. The Lagrange multiplier is 1.500050e+04.
Because there are no lower bounds, upper bounds, or linear equality constraints, the only meaningful Lagrange multiplier is lambda.ineqlin. Because lambda.ineqlin is nonzero, you can tell that the inequality constraint is active. Evaluate the constraint to see that the solution is on the boundary.
fprintf('The linear inequality constraint A*x has value %d.\n',A*x)The linear inequality constraint A*x has value 9.150244e-08.
The sum of the solution components is zero to within tolerances.
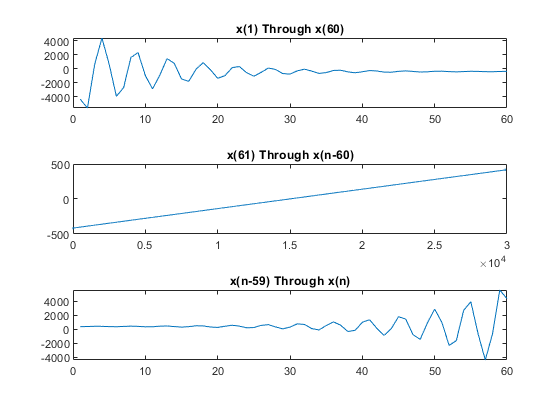
The solution x has three regions: an initial portion, a final portion, and an approximately linear portion over most of the solution. Plot the three regions.
subplot(3,1,1) plot(x(1:60)) title('x(1) Through x(60)') subplot(3,1,2) plot(x(61:n-60)) title('x(61) Through x(n-60)') subplot(3,1,3) plot(x(n-59:n)) title('x(n-59) Through x(n)')