Estimate Transfer Function Models in the System Identification App
Use the app to set model configuration and estimation options for estimating a transfer function model.
In the System Identification app, select Estimate > Transfer Function Models
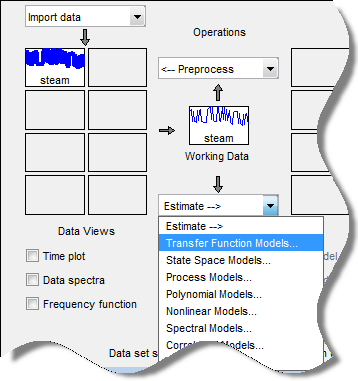
The Transfer Functions dialog box opens.
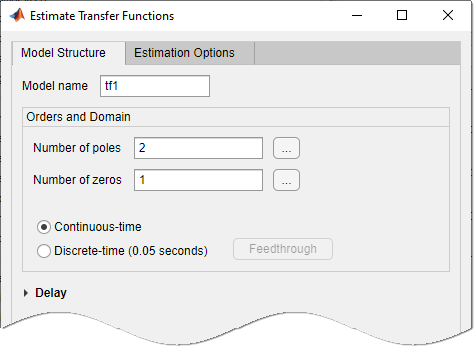
Tip
For more information on the options in the dialog box, click Help.
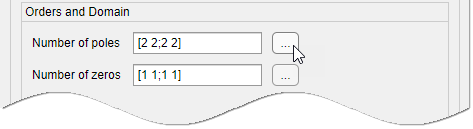
In the Number of poles and Number of zeros fields, specify the number of poles and zeros of the transfer function as nonnegative integers.
Select Continuous-time or Discrete-time to specify whether the model is a continuous- or discrete-time transfer function.
For discrete-time models, the number of poles and zeros refers to the roots of the numerator and denominator polynomials expressed in terms of the lag variable
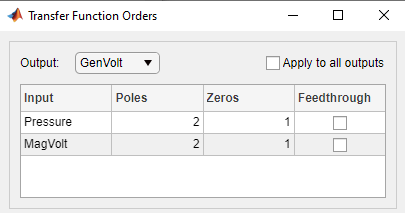
q^-1.(For discrete-time models only) Specify whether to estimate the model feedthrough. Select the Feedthrough check box.

A discrete-time model with 2 poles and 3 zeros takes the following form:
When the model has direct feedthrough,
b0is a free parameter whose value is estimated along with the rest of the model parametersb1,b2,b3,a1,a2. When the model has no feedthrough,b0is fixed to zero.Expand the Delay section to specify nominal values and constraints for transport delays for different input/output pairs.
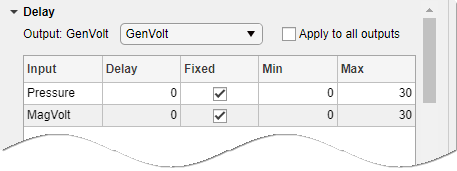
Use the Output list to select an output. Select the Fixed check box to specify a transport delay as a fixed value. Specify its nominal value in the Delay field.
Expand the Estimation Options section to specify estimation options.
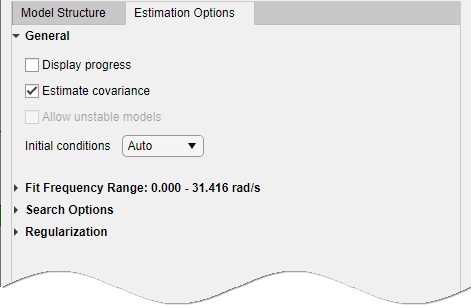
Select Display progress to view the progress of the optimization.
Select Estimate covariance to estimate the covariance of the transfer function parameters.
(For frequency-domain data only) Specify whether to allow the estimation process to use parameter values that may lead to unstable models. Select the Allow unstable models option. An unstable model is delivered only if it produces a better fit to the data than other stable models computed during the estimation process.
Specify how to treat the initial conditions in the Initial condition list. For more information, see Specifying Initial Conditions for Iterative Estimation of Transfer Functions.
Expand Fit Frequency Range and set the range sliders to the desired passband to specify the frequency range over which the transfer function model must fit the data. By default the entire frequency range (0 to Nyquist frequency) is covered.

Expand Search Options to specify options for controlling the search iterations.
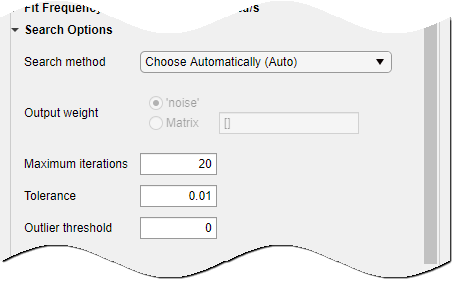
Expand Regularization to obtain regularized estimates of model parameters. Specify the regularization constants Lambda and R.

To learn more about regularization, see Regularized Estimates of Model Parameters.
Click Estimate to estimate the model. A new model gets added to the System Identification app.