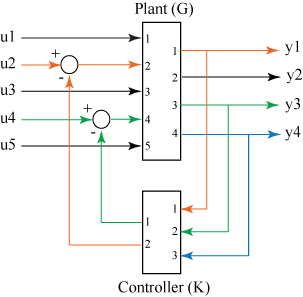
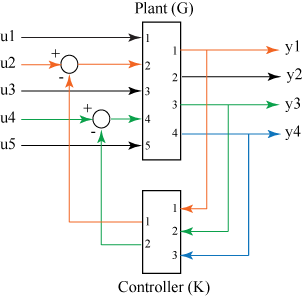
feedback
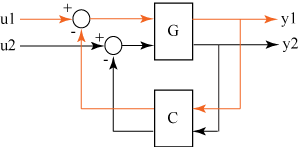
Feedback connection of multiple models
Syntax
Description
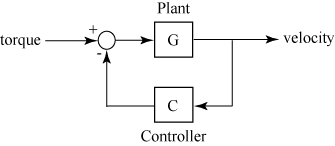
sys = feedback(sys1,sys2)sys for the negative feedback interconnection of
model objects sys1,sys2.
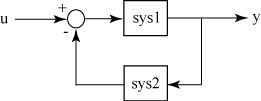
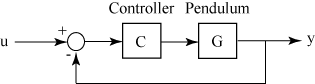
From the figure, the closed-loop model sys has
u as input vector and y as output vector. Both
models, sys1 and sys2, must either be continuous or
discrete with identical sample times.
Examples
Input Arguments
Output Arguments
Limitations
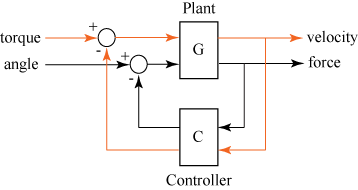
The feedback connection must be free of algebraic loops. For instance, if D1 and D2 are the feedthrough matrices of
sys1andsys2, this condition is equivalent to:I + D1D2 nonsingular when using negative feedback
I − D1D2 nonsingular when using positive feedback
Version History
Introduced before R2006a