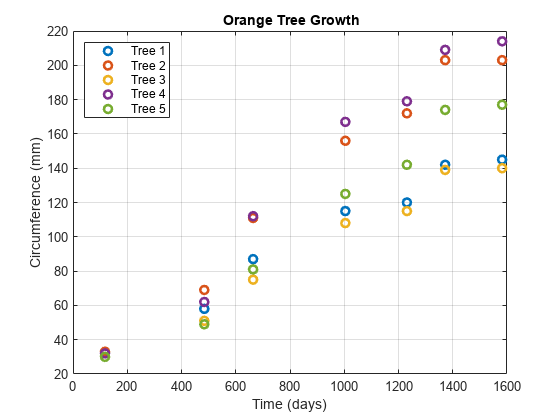
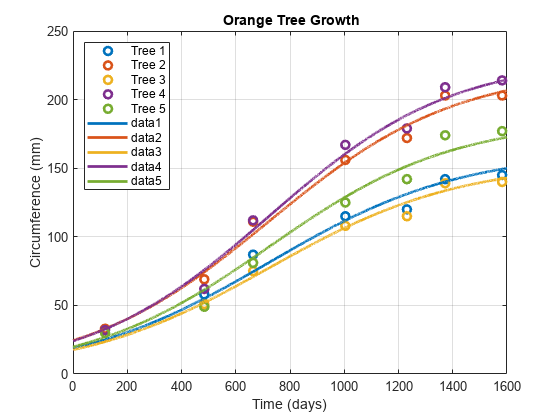
nlmefit
Nonlinear mixed-effects estimation
Syntax
beta = nlmefit(X,y,group,V,fun,beta0)
[beta,PSI] = nlmefit(X,y,group,V,fun,beta0)
[beta,PSI,stats] = nlmefit(X,y,group,V,fun,beta0)
[beta,PSI,stats,B] = nlmefit(X,y,group,V,fun,beta0)
[beta,PSI,stats,B] = nlmefit(X,y,group,V,fun,beta0,'Name',value)
Description
beta = nlmefit(X,y,group,V,fun,beta0) fits
a nonlinear mixed-effects regression model and returns estimates of
the fixed effects in beta. By default, nlmefit fits
a model in which each parameter is the sum of a fixed and a random
effect, and the random effects are uncorrelated (their covariance
matrix is diagonal).
X is an n-by-h matrix
of n observations on h predictors.
y is an n-by-1 vector
of responses.
group is a grouping variable indicating m groups in the
observations. group is a categorical variable, a numeric vector, a character
matrix with rows for group names, a string array, or a cell array of character vectors. For more
information on grouping variables, see Grouping Variables.
V is an m-by-g matrix
or cell array of g group-specific predictors. These
are predictors that take the same value for all observations in a
group. The rows of V are assigned to groups using grp2idx, according to the order specified
by grp2idx(group). Use a cell array for V if
group predictors vary in size across groups. Use [] for V if
there are no group-specific predictors.
fun is a handle to a function that accepts
predictor values and model parameters and returns fitted values. fun has
the form
yfit = modelfun(PHI,XFUN,VFUN)
The arguments are:
PHI— A 1-by-p vector of model parameters.XFUN— A k-by-h array of predictors, where:k = 1 if
XFUNis a single row ofX.k = ni if
XFUNcontains the rows ofXfor a single group of size ni.k = n if
XFUNcontains all rows ofX.
VFUN— Group-specific predictors given by one of:A 1-by-g vector corresponding to a single group and a single row of
V.An n-by-g array, where the jth row is V(
I,:) if the jth observation is in groupI.
If
Vis empty,nlmefitcallsmodelfunwith only two inputs.yfit— A k-by-1 vector of fitted values
When either PHI or VFUN contains
a single row, it corresponds to all rows in the other two input arguments.
Note
If modelfun can compute yfit for
more than one vector of model parameters per call, use the 'Vectorization' parameter
(described later) for improved performance.
beta0 is a q-by-1 vector
with initial estimates for q fixed effects. By
default, q is the number of model parameters p.
nlmefit fits the model by maximizing an
approximation to the marginal likelihood with random effects integrated
out, assuming that:
Random effects are multivariate normally distributed and independent between groups.
Observation errors are independent, identically normally distributed, and independent of the random effects.
[beta,PSI] = nlmefit(X,y,group,V,fun,beta0) also
returns PSI, an r-by-r estimated
covariance matrix for the random effects. By default, r is
equal to the number of model parameters p.
[beta,PSI,stats] = nlmefit(X,y,group,V,fun,beta0) also
returns stats, a structure with fields:
dfe— The error degrees of freedom for the modellogl— The maximized loglikelihood for the fitted modelrmse— The square root of the estimated error variance (computed on the log scale for theexponentialerror model)errorparam— The estimated parameters of the error variance modelaic— The Akaike information criterion, calculated asaic= -2 *logl+ 2 *numParam, wherenumParamis the number of fitting parameters, including the degree of freedom for covariance matrix of the random effects, the number of fixed effects and the number of parameters of the error model, andloglis a field in thestatsstructurebic— The Bayesian information criterion, calculated asbic= –2*logl+ log(M) *numParamMis the number of groups.numParamandloglare defined as inaic.
Note that some literature suggests that the computation of
bicshould be ,bic= –2*logl+ log(N) *numParam, whereNis the number of observations.covb— The estimated covariance matrix of the parameter estimatessebeta— The standard errors forbetaires— The population residuals(y-y_population), wherey_populationis the individual predicted valuespres— The population residuals(y-y_population), wherey_populationis the population predicted valuesiwres— The individual weighted residualspwres— The population weighted residualscwres— The conditional weighted residuals
[beta,PSI,stats,B] = nlmefit(X,y,group,V,fun,beta0) also
returns B, an r-by-m matrix
of estimated random effects for the m groups. By
default, r is equal to the number of model parameters p.
[beta,PSI,stats,B] = nlmefit(X,y,group,V,fun,beta0,' specifies
one or more optional parameter name/value pairs. Specify Name',value)Name inside
single quotes.
Use the following parameters to fit a model different from the
default. (The default model is obtained by setting both FEConstDesign and REConstDesign to eye(p),
or by setting both FEParamsSelect and REParamsSelect to 1:p.)
Use at most one parameter with an 'FE' prefix
and one parameter with an 'RE' prefix. The nlmefit function
requires you to specify at least one fixed effect and one random effect.
| Parameter | Value |
|---|---|
FEParamsSelect | A vector specifying which elements of the parameter vector |
FEConstDesign | A p-by-q design
matrix |
FEGroupDesign | A p-by-q-by-m array specifying a different p-by-q fixed-effects design matrix for each of the m groups. |
FEObsDesign | A p-by-q-by-n array specifying a different p-by-q fixed-effects design matrix for each of the n observations. |
REParamsSelect | A vector specifying which elements of the parameter vector |
REConstDesign | A p-by-r design
matrix |
REGroupDesign | A p-by-r-by-m array specifying a different p-by-r random-effects design matrix for each of m groups. |
REObsDesign | A p-by-r-by-n array specifying a different p-by-r random-effects design matrix for each of n observations. |
Use the following parameters to control the iterative algorithm for maximizing the likelihood:
Parameter | Value |
|---|---|
RefineBeta0 | Determines whether |
ErrorModel | A character vector or string scalar specifying the form of the error term. Default is
If this parameter is given, the output
|
ApproximationType | The method used to approximate the likelihood of the model. Choices are:
|
Vectorization | Indicates acceptable sizes for the
|
CovParameterization | Specifies the parameterization used internally for the
scaled covariance matrix. Choices are |
CovPattern | Specifies an r-by-r logical
or numeric matrix Alternatively, |
ParamTransform | A vector of p-values specifying
a transformation function f() for each of the
|
Options | A structure of the form returned by
|
OptimFun | Optimization function for the estimation process that maximizes a likelihood function,
specified as |
Examples
References
[1] Lindstrom, M. J., and D. M. Bates. “Nonlinear mixed-effects models for repeated measures data.” Biometrics. Vol. 46, 1990, pp. 673–687.
[2] Davidian, M., and D. M. Giltinan. Nonlinear Models for Repeated Measurements Data. New York: Chapman & Hall, 1995.
[3] Pinheiro, J. C., and D. M. Bates. “Approximations to the log-likelihood function in the nonlinear mixed-effects model.” Journal of Computational and Graphical Statistics. Vol. 4, 1995, pp. 12–35.
[4] Demidenko, E. Mixed Models: Theory and Applications. Hoboken, NJ: John Wiley & Sons, Inc., 2004.
Version History
Introduced in R2008b