moment
Central moment
Description
m = moment(X,order)X for the order specified by
order.
If
Xis a vector, thenmoment(X,order)returns a scalar value that is the k-order central moment of the elements inX.If
Xis a matrix, thenmoment(X,order)returns a row vector containing the k-order central moment of each column inX.If
Xis a multidimensional array, thenmoment(X,order)operates along the first nonsingleton dimension ofX.
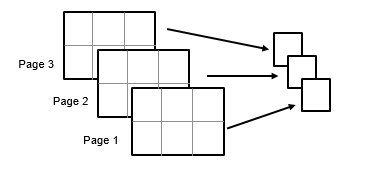
m = moment(X,order,vecdim)vecdim. For example, if X is a 2-by-3-by-4
array, then moment(X,1,[1 2]) returns a 1-by-1-by-4 array. Each
element of the output array is the first-order central moment of the elements on the
corresponding page of X.
Examples
Input Arguments
Output Arguments
Algorithms
The central moment of order k for a distribution is defined as
where µ is the mean of x, and
E(t) represents the expected value of the
quantity t. The moment function computes a sample
version of this population value.
Note that the first-order central moment is zero, and the second-order central moment
is the variance computed using a divisor of n rather than
n – 1, where n is the length of the vector
x or the number of rows in the matrix
X.
Extended Capabilities
Version History
Introduced before R2006a