Generalized Pareto Distribution
Definition
The probability density function for the generalized Pareto distribution with shape parameter k ≠ 0, scale parameter σ, and threshold parameter θ, is
for θ < x, when k > 0, or for θ < x < θ – σ/k when k < 0.
For k = 0, the density is
for θ < x.
If k = 0 and θ = 0, the generalized Pareto distribution is equivalent to the exponential distribution. If k > 0 and θ = σ/k, the generalized Pareto distribution is equivalent to the Pareto distribution with a scale parameter equal to σ/k and a shape parameter equal to 1/k.
Background
Like the exponential distribution, the generalized Pareto distribution is often used to model the tails of another distribution. For example, you might have washers from a manufacturing process. If random influences in the process lead to differences in the sizes of the washers, a standard probability distribution, such as the normal, could be used to model those sizes. However, while the normal distribution might be a good model near its mode, it might not be a good fit to real data in the tails and a more complex model might be needed to describe the full range of the data. On the other hand, only recording the sizes of washers larger (or smaller) than a certain threshold means you can fit a separate model to those tail data, which are known as exceedances. You can use the generalized Pareto distribution in this way, to provide a good fit to extremes of complicated data.
The generalized Pareto distribution allows a continuous range of possible shapes that includes both the exponential and Pareto distributions as special cases. You can use either of those distributions to model a particular dataset of exceedances. The generalized Pareto distribution allows you to “let the data decide” which distribution is appropriate.
The generalized Pareto distribution has three basic forms, each corresponding to a limiting distribution of exceedance data from a different class of underlying distributions.
Distributions whose tails decrease exponentially, such as the normal, lead to a generalized Pareto shape parameter of zero.
Distributions whose tails decrease as a polynomial, such as Student's t, lead to a positive shape parameter.
Distributions whose tails are finite, such as the beta, lead to a negative shape parameter.
The generalized Pareto distribution is used in the tails of distribution fit
objects of the paretotails object.
Parameters
Fit Generalized Pareto Distribution
Generate a large number of random values from a Student's t distribution with 5 degrees of freedom, and then discard everything less than 2. Fit a generalized Pareto distribution to those exceedances.
rng("default") % For reproducibility t = trnd(5,5000,1); y = t(t > 2) - 2; paramEsts = gpfit(y)
paramEsts = 1×2
0.1445 0.7225
Notice that the shape parameter estimate (the first element) is positive, which is what you would expect based on exceedances from a Student's t distribution.
h = histogram(y+2,2:0.5:12);
h.FaceColor = [0.8 0.8 1];
xgrid = linspace(2,12,1000);
line(xgrid,0.5*length(y)* ...
gppdf(xgrid,paramEsts(1),paramEsts(2),2));
xlim([2 12])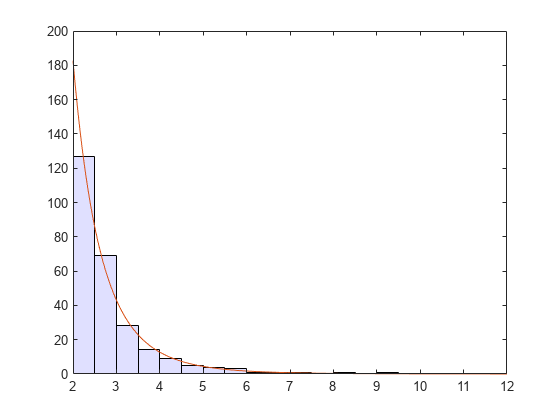
Examples
Compute Generalized Pareto Distribution pdf
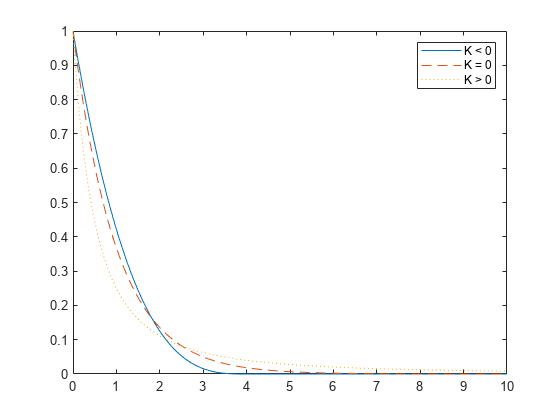
Compute the pdf of three generalized Pareto distributions. The first has shape parameter k = -0.25, the second has k = 0, and the third has k = 1.
x = linspace(0,10,1000); y1 = gppdf(x,-.25,1,0); y2 = gppdf(x,0,1,0); y3 = gppdf(x,1,1,0);
Plot the three pdfs on the same figure.
figure; plot(x,y1,'-', x,y2,'--', x,y3,':') legend({'K < 0' 'K = 0' 'K > 0'});
References
[1] Embrechts, P., C. Klüppelberg, and T. Mikosch. Modelling Extremal Events for Insurance and Finance. New York: Springer, 1997.
[2] Kotz, S., and S. Nadarajah. Extreme Value Distributions: Theory and Applications. London: Imperial College Press, 2000.
