bootci
Bootstrap confidence interval
Syntax
Description
ci = bootci(nboot,bootfun,d1,...,dN)d1,...,dN. These nonscalar arguments must have the same
number of rows. The bootci function passes the samples of nonscalar
data and the unchanged scalar data arguments in d1,...,dN to
bootfun.
ci = bootci(nboot,{bootfun,d1,...,dN},Name,Value)'Alpha'
name-value argument.
Note that you must pass the bootfun and
d1,...,dN arguments to bootci as a single cell
array.
Examples
Bootstrap Confidence Interval
Compute the confidence interval for the capability index in statistical process control.
Generate 30 random numbers from the normal distribution with mean 1 and standard deviation 1.
rng('default') % For reproducibility y = normrnd(1,1,30,1);
Specify the lower and upper specification limits of the process. Define the capability index.
LSL = -3; USL = 3; capable = @(x)(USL-LSL)./(6*std(x));
Compute the 95% confidence interval for the capability index by using 2000 bootstrap samples. By default, bootci uses the bias corrected and accelerated percentile method to construct the confidence interval.
ci = bootci(2000,capable,y)
ci = 2×1
0.5937
0.9900
Compute the studentized confidence interval for the capability index.
sci = bootci(2000,{capable,y},'Type','student')sci = 2×1
0.5193
0.9930
Bootstrap Confidence Intervals for Nonlinear Regression Model Coefficients
Compute bootstrap confidence intervals for the coefficients of a nonlinear regression model. The technique used in this example involves bootstrapping the predictor and response values, and assumes that the predictor variable is random. For a technique that assumes the predictor variable is fixed and bootstraps the residuals, see Bootstrap Confidence Intervals for Linear Regression Model Coefficients.
Note: This example uses nlinfit, which is useful when you only need the coefficient estimates or residuals of a nonlinear regression model and you need to repeat fitting a model multiple times, as in the case of bootstrapping. If you need to investigate a fitted regression model further, create a nonlinear regression model object by using fitnlm. You can create confidence intervals for the coefficients of the resulting model by using the coefCI object function, although this function does not use bootstrapping.
Generate data from the nonlinear regression model , where , , and are coefficients; the predictor variable x is exponentially distributed with mean 2; and the error term is normally distributed with mean 0 and standard deviation 0.1.
modelfun = @(b,x)(b(1)+b(2)*exp(-b(3)*x)); rng('default') % For reproducibility b = [1;3;2]; x = exprnd(2,100,1); y = modelfun(b,x) + normrnd(0,0.1,100,1);
Create a function handle for the nonlinear regression model that uses the initial values in beta0.
beta0 = [2;2;2]; beta = @(predictor,response)nlinfit(predictor,response,modelfun,beta0)
beta = function_handle with value:
@(predictor,response)nlinfit(predictor,response,modelfun,beta0)
Compute the 95% bootstrap confidence intervals for the coefficients of the nonlinear regression model. Create the bootstrap samples from the generated data x and y.
ci = bootci(1000,beta,x,y)
ci = 2×3
0.9821 2.9552 2.0180
1.0410 3.1623 2.2695
The first two confidence intervals include the true coefficient values and , respectively. However, the third confidence interval does not include the true coefficient value .
Now compute the 99% bootstrap confidence intervals for the model coefficients.
newci = bootci(1000,{beta,x,y},'Alpha',0.01)newci = 2×3
0.9730 2.9112 1.9562
1.0469 3.1876 2.3133
All three confidence intervals include the true coefficient values.
Bootstrap Confidence Intervals for Linear Regression Model Coefficients
Compute bootstrap confidence intervals for the coefficients of a linear regression model. The technique used in this example involves bootstrapping the residuals and assumes that the predictor variable is fixed. For a technique that assumes the predictor variable is random and bootstraps the predictor and response values, see Bootstrap Confidence Intervals for Nonlinear Regression Model Coefficients.
Note: This example uses regress, which is useful when you only need the coefficient estimates or residuals of a regression model and you need to repeat fitting a model multiple times, as in the case of bootstrapping. If you need to investigate a fitted regression model further, create a linear regression model object by using fitlm. You can create confidence intervals for the coefficients of the resulting model by using the coefCI object function, although this function does not use bootstrapping.
Load the sample data.
load haldPerform a linear regression and compute the residuals.
x = [ones(size(heat)),ingredients]; y = heat; b = regress(y,x); yfit = x*b; resid = y - yfit;
Compute the 95% bootstrap confidence intervals for the coefficients of the linear regression model. Create the bootstrap samples from the residuals. Use normal approximated intervals with bootstrapped bias and standard error by specifying 'Type','normal'. You cannot use the default confidence interval type in this case.
ci = bootci(1000,{@(bootr)regress(yfit+bootr,x),resid}, ...
'Type','normal')ci = 2×5
-47.7130 0.3916 -0.6298 -1.0697 -1.2604
172.4899 2.7202 1.6495 1.2778 0.9704
Plot the estimated coefficients b, omitting the intercept term, and display error bars showing the coefficient confidence intervals.
slopes = b(2:end)';
lowerBarLengths = slopes-ci(1,2:end);
upperBarLengths = ci(2,2:end)-slopes;
errorbar(1:4,slopes,lowerBarLengths,upperBarLengths)
xlim([0 5])
title('Coefficient Confidence Intervals')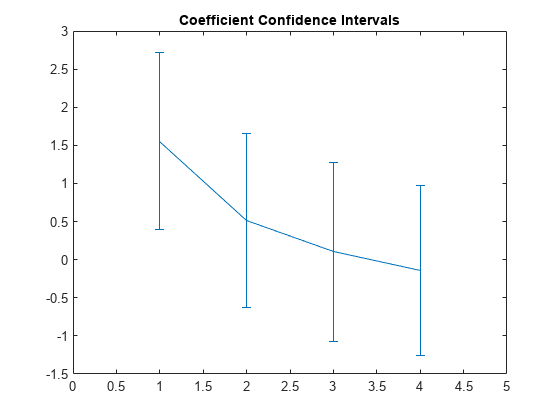
Only the first nonintercept coefficient is significantly different from 0.
Confidence Intervals for Multiple Statistics
Compute the mean and standard deviation of 100 bootstrap samples. Find the 95% confidence interval for each statistic.
Generate 100 random numbers from the exponential distribution with mean 5.
rng('default') % For reproducibility y = exprnd(5,100,1);
Draw 100 bootstrap samples from the vector y. For each bootstrap sample, compute the mean and standard deviation. Find the 95% bootstrap confidence interval for the mean and standard deviation.
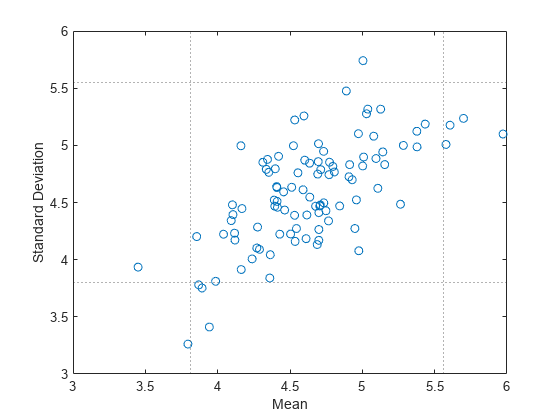
[ci,bootstat] = bootci(100,@(x)[mean(x) std(x)],y);
ci(:,1) contains the lower and upper bounds of the mean confidence interval, and c(:,2) contains the lower and upper bounds of the standard deviation confidence interval. Each row of bootstat contains the mean and standard deviation of a bootstrap sample.
Plot the mean and standard deviation of each bootstrap sample as a point. Plot the lower and upper bounds of the mean confidence interval as dotted vertical lines, and plot the lower and upper bounds of the standard deviation confidence interval as dotted horizontal lines.
plot(bootstat(:,1),bootstat(:,2),'o') xline(ci(1,1),':') xline(ci(2,1),':') yline(ci(1,2),':') yline(ci(2,2),':') xlabel('Mean') ylabel('Standard Deviation')
Input Arguments
nboot — Number of bootstrap samples
positive integer scalar
Number of bootstrap samples to draw, specified as a positive integer scalar. To
create each bootstrap sample, bootci randomly selects with
replacement n out of the n rows of nonscalar data
in d or d1,...,dN.
Example: 100
Data Types: single | double
bootfun — Function to apply to each sample
function handle
Function to apply to each sample, specified as a function handle. The function can
be a custom or built-in function. You must specify bootfun with the
@ symbol.
Example: @mean
Data Types: function_handle
d — Data to sample from
column vector | matrix
Data to sample from, specified as a column vector or matrix. The
n rows of d correspond to observations. When
you use multiple data input arguments d1,...,dN, you can specify some
arguments as scalar values, but all nonscalar arguments must have the same number of
rows.
If you use a single vector argument d, you can specify it as a
row vector. bootci then samples from the elements of the
vector.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: bootci(100,{@mean,1:6'},'Alpha',0.1) specifies to draw 100
bootstrap samples from the values 1 through 6, take the mean of each sample, and then
compute the 90% confidence interval for the sample mean.
Alpha — Significance level
0.05 (default) | positive scalar in (0,1)
Significance level, specified as a positive scalar between 0 and 1.
bootci computes the 100*(1-Alpha) bootstrap
confidence interval of each statistic defined by the function
bootfun.
Example: 'Alpha',0.01
Data Types: single | double
Type — Confidence interval type
'bca' (default) | 'norm' | 'per' | 'cper' | 'stud' | ...
Confidence interval type, specified as one of the values in this table.
| Value | Description |
|---|---|
'norm' or 'normal' | Normal approximated interval with bootstrapped bias and standard error [1] |
'per' or 'percentile' | Basic percentile method |
'cper' or 'corrected
percentile' | Bias corrected percentile method [2] |
'bca' | Bias corrected and accelerated percentile method [3], [4]. This method involves a z0 factor computed using the proportion of bootstrap values that are less than the original sample value. To produce reasonable results when the sample is lumpy, the software computes z0 by including half of the bootstrap values that are the same as the original sample value. |
'stud' or 'student' | Studentized confidence interval [3] |
Example: 'Type','student'
NBootStd — Number of bootstrap samples for studentized standard error estimate
100 (default) | positive integer scalar
Number of bootstrap samples for the studentized standard error estimate, specified as a positive integer scalar.
bootci computes the studentized bootstrap confidence interval
of the statistic defined by the function bootfun, and estimates
the standard error of the bootstrap statistics by using NBootStd
bootstrap data samples.
Note
To use this name-value argument, the Type value must be
'stud' or 'student'. Specify either
NBootStd or StdErr, but not both.
Example: 'NBootStd',50
Data Types: single | double
StdErr — Function used to compute studentized standard error estimate
function handle
Function used to compute the studentized standard error estimate, specified as a function handle.
bootci computes the studentized bootstrap confidence interval
of the statistic defined by the function bootfun, and estimates
the standard error of the bootstrap statistics by using the function
StdErr. The StdErr function must take the
same arguments as bootfun and return the standard error of the
statistic computed by bootfun.
Note
To use this name-value argument, the Type value must be
'stud' or 'student'. Specify either
NBootStd or StdErr, but not both.
Example: 'StdErr',@std
Data Types: function_handle
Weights — Observation weights
ones(n,1)/n (default) | nonnegative vector
Observation weights, specified as a nonnegative vector with at least one positive
element. The number of elements in Weights must be equal to the
number of rows n in the data d or
d1,...,dN. To obtain one bootstrap sample,
bootci randomly selects with replacement n
out of n rows of data using these weights as multinomial sampling
probabilities.
Data Types: single | double
Options — Options for computing in parallel and setting random streams
structure
Options for computing in parallel and setting random streams, specified as a
structure. Create the Options structure using statset. This table lists the option fields and their
values.
| Field Name | Value | Default |
|---|---|---|
UseParallel | Set this value to true to run computations in
parallel. | false |
UseSubstreams | Set this value to To compute
reproducibly, set | false |
Streams | Specify this value as a RandStream object or
cell array of such objects. Use a single object except when the
UseParallel value is true
and the UseSubstreams value is
false. In that case, use a cell array that
has the same size as the parallel pool. | If you do not specify Streams, then
bootci uses the default stream or
streams. |
Note
You need Parallel Computing Toolbox™ to run computations in parallel.
Example: Options=statset(UseParallel=true,UseSubstreams=true,Streams=RandStream("mlfg6331_64"))
Data Types: struct
Output Arguments
ci — Confidence interval bounds
vector with two rows | matrix with two rows | multidimensional array with two rows
Confidence interval bounds, returned as a vector, matrix, or multidimensional array with two rows.
If
bootfunreturns a scalar, thenciis a vector containing the lower and upper bounds of the confidence interval.If
bootfunreturns a vector of length m, thenciis a matrix of size 2-by-m, whereci(1,:)are lower bounds andci(2,:)are upper bounds.If
bootfunreturns a multidimensional array, thenciis an array, whereci(1,:,...)is an array of lower bounds andci(2,:,...)is an array of upper bounds.
bootstat — Bootstrap statistics
column vector | matrix
Bootstrap statistics, returned as a column vector or matrix with
nboot rows. The ith row of
bootstat corresponds to the results of applying
bootfun to the ith bootstrap sample. If
bootfun returns a matrix or array, then the
bootci function first converts this output to a row vector before
storing it in bootstat.
References
[1] Davison, A. C., and D. V. Hinkley. Bootstrap Methods and Their Applications. Cambridge University Press, 1997.
[2] Efron, Bradley. The Jackknife, the Bootstrap and Other Resampling Plans. Philadelphia: The Society for Industrial and Applied Mathematics, 1982.
[3] DiCiccio, Thomas J., and Bradley Efron. “Bootstrap Confidence Intervals.” Statistical Science 11, no. 3 (1996): 189–228.
[4] Efron, Bradley, and Robert J. Tibshirani. An Introduction to the Bootstrap. New York: Chapman & Hall, 1993.
Extended Capabilities
Automatic Parallel Support
Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.
To run in parallel, specify the Options name-value argument in the call to
this function and set the UseParallel field of the
options structure to true using
statset:
Options=statset(UseParallel=true)
For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Version History
Introduced in R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)