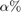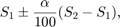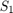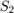midcross
Mid-reference level crossing for bilevel waveform
Syntax
Description
c = midcross(x)x crosses the 50% reference level. To determine the
transitions, the midcross function estimates the state levels
of x by a histogram method and identifies all intervals which
cross the upper-state boundary of the low state and the lower-state boundary of the
high state.
c = midcross(x,Name,Value)
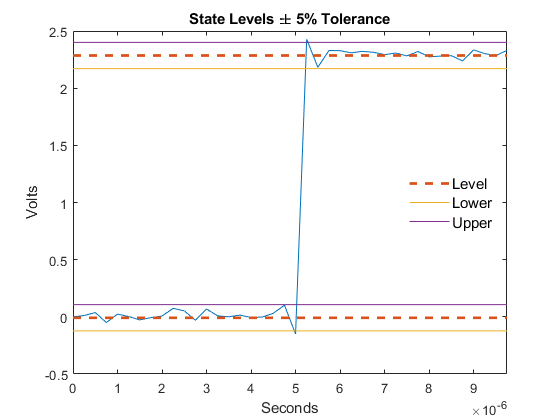
midcross(___) plots the signal and marks the
location of the mid-crossings (mid-reference level instants) and the associated
reference levels. The function also plots the state levels with upper and lower
state boundaries.
Examples
Input Arguments
Output Arguments
More About
References
[1] IEEE® Standard on Transitions, Pulses, and Related Waveforms, IEEE Standard 181, 2003. p. 20.
Extended Capabilities
Version History
Introduced in R2012a
See Also
falltime | pulsewidth | risetime | settlingtime | statelevels