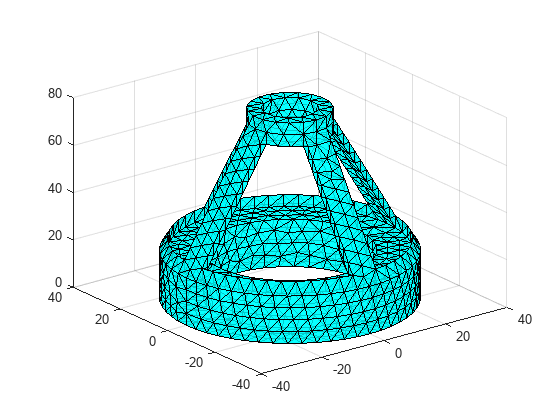
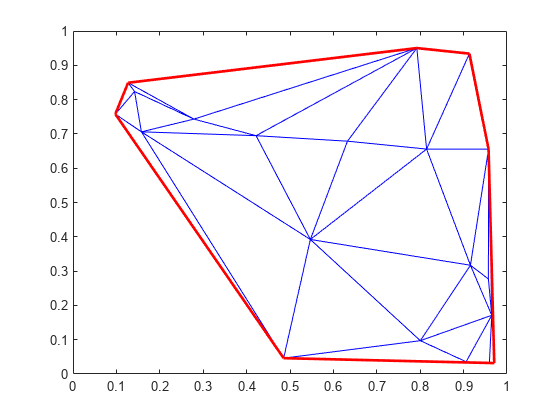
freeBoundary
(Not recommended) Free boundary facets
freeBoundary(TriRep) is not recommended. Use freeBoundary(triangulation) instead.
TriRep is not recommended. Use triangulation instead.
Description
Examples
Input Arguments
Output Arguments
More About
Extended Capabilities
Version History
Introduced in R2009a
See Also
delaunayTriangulation | convexHull | featureEdges | faceNormal | triangulation